古典密码
仿射密码
仿射密码为单表加密的一种,字母系统中所有字母都藉一简单数学方程加密,对应至数值,或转回字母。
输入内容
输入的内容可能包含大写,小写和特殊字符,此时可以分别进行加解密,通过调用python的isupper(),islower()函数来判断。
大写字母加密/解密后的结果仍是大写字母,小写字母加密/解密后的结果仍是小写字母 。特殊字符不做处理,直接照搬。
加密算法
$$
c_i=(k_1⋅m_i+k_2)mod26
$$
前提条件:
$$
gcd(k_1,26)=1
$$
假如不满足该条件,则不同的密文字符可以对应多个明文字符。
所以我们首先需要写一个求两个数最大公因数的函数,此处用辗转相除法。
1 | #辗转相除法 |
判断条件可以写在主函数中。
如果满足不满足条件,就请求重新执行该程序。
加密函数如下
1 | #加密函数 |
解密算法
$$
m_i=k_1^{−1}⋅(c_i−k_2)mod26
$$
同样需要先判断k1是否与26互素。
与加密的步骤不同的是这里多了一个求逆的过程。
此处使用扩展欧几里得算法。
1 | #求a关于m的逆元 |
那么,解密函数如下
1 | #解密函数 |
运行结果
加密样例
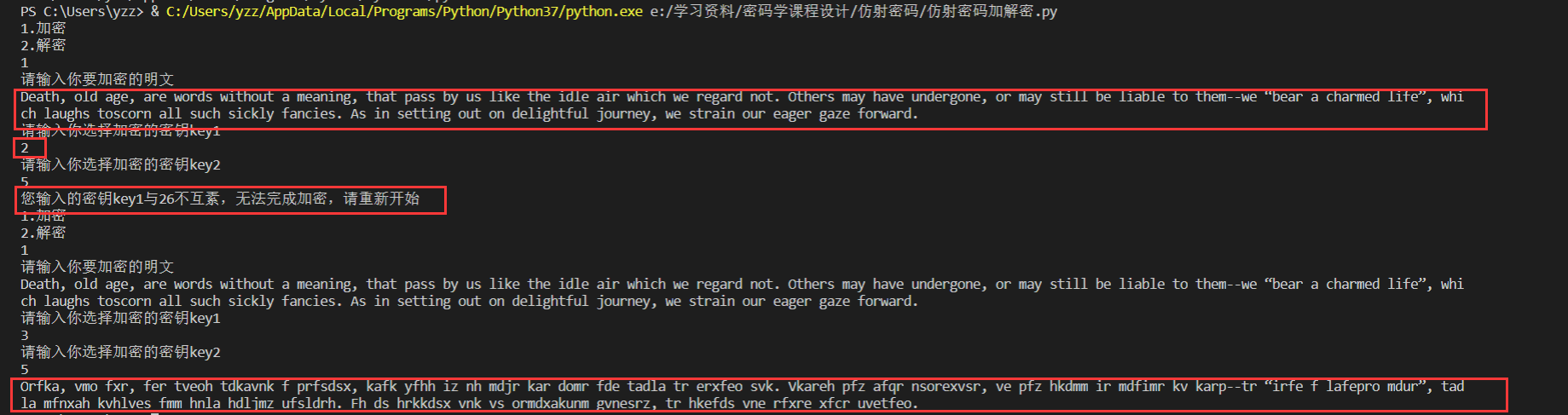
解密样例

枚举法破解
暴力破解直接附代码
1 | def EnumerationMethod(cipher): |
统计分析法破解
最好截取的密文长度足够长,同时已知的自然语言字符统计规律。

由图已知使用频率最高的字母为e,那么我们就可以先找出密文当中出现次数最多的那个字母。
1 | #字典方式找出现次数最多的字母 |
用字典方法有一个缺陷就是可能输入的密文带空格,最后可能找到的是空格,所以用replace()函数把空格删去,再进行统计。
然后用两个循环找key1和key2满足出现次数最多的那个字母对应明文为e的情况。
1 | #统计分析法 |
最后可以在运行结果中找到合乎语法的正确明文。
运行结果
暴力破解
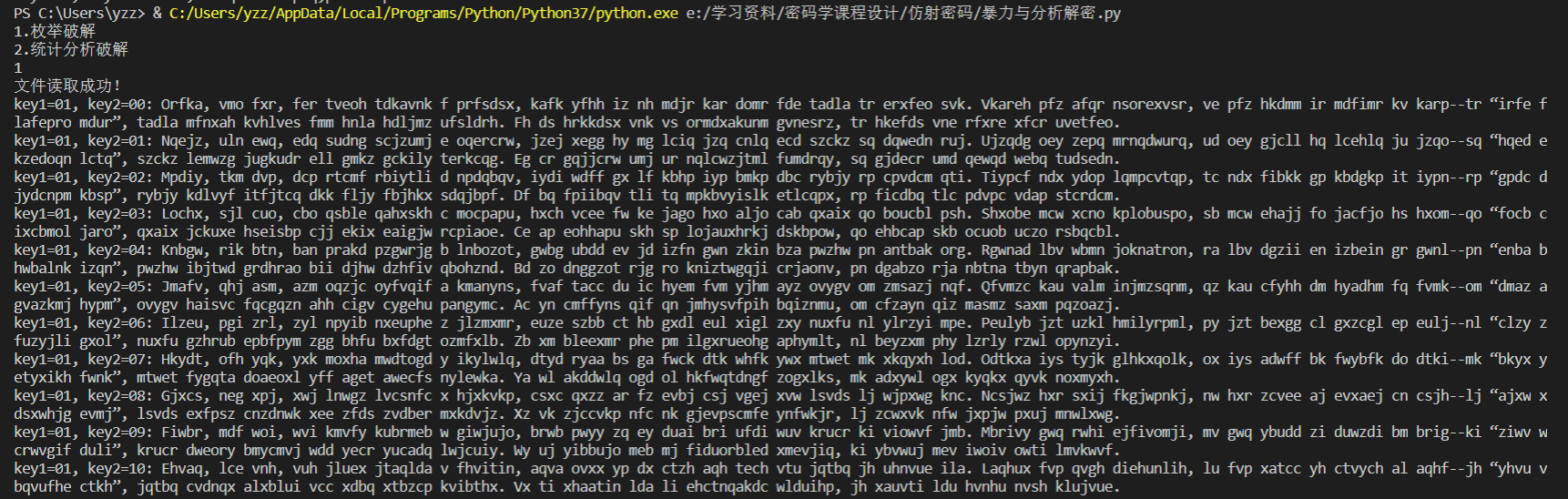
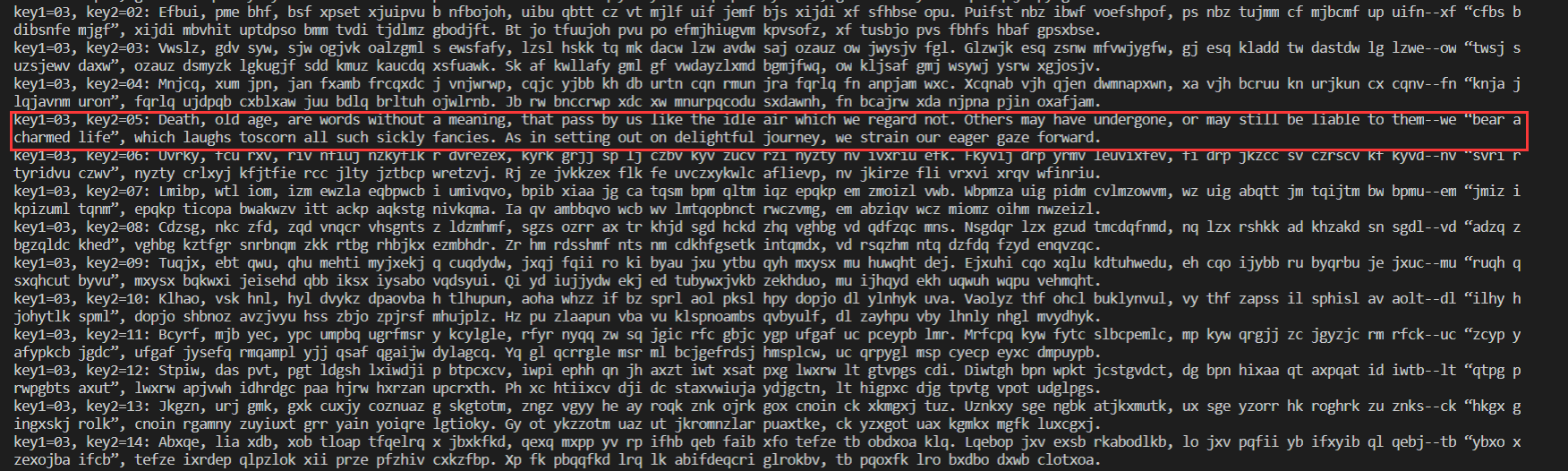
统计分析**
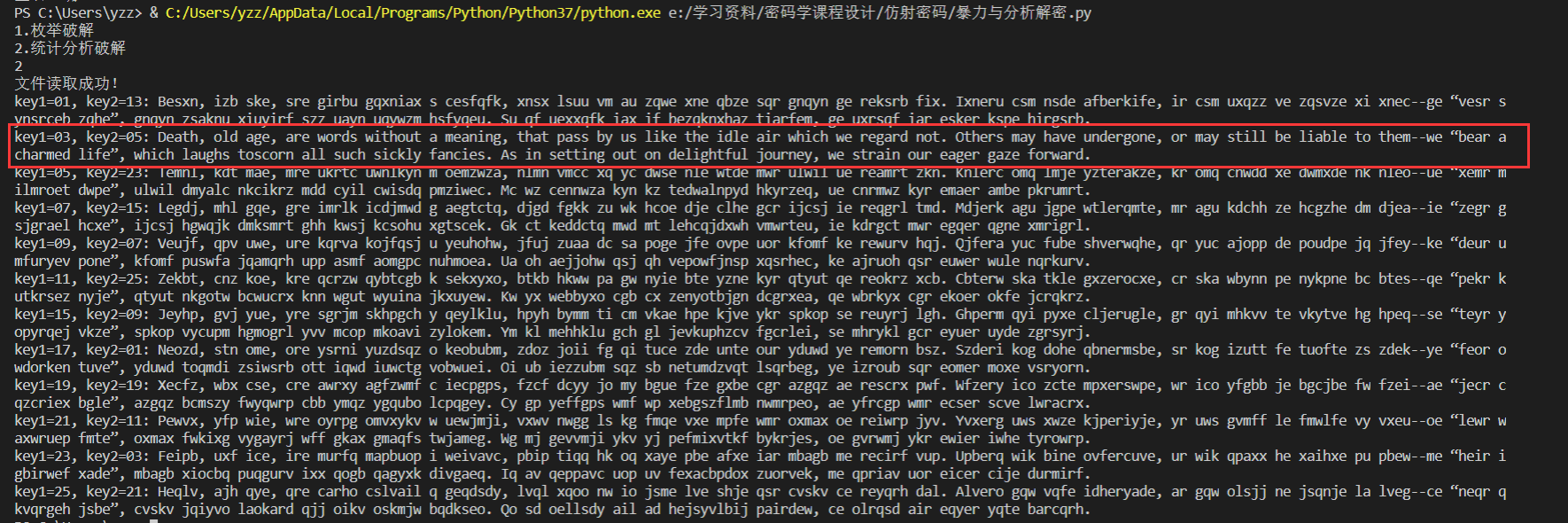
安全性分析
仿射密码属于单表代换密码,单表代换密码的密钥空间很小,同时它没有将字母出现的统计规律隐藏起来,因此使用统计分析法很快就可以进行破解。从这一点来说,汉语在加密方面的特性要远远优于英语,汉语中常用汉字就有3755个,而英语只有26个英文字母。
仿射密码加密算法为
$$
ye(x){\equiv}ax+b(mod26) 其中要求gcd(a,26)=1
$$
满足条件的a有12个,而b有26个,所以仿射加密的密钥空间大小为12*26=312。对于312种情况,现在的计算机通过暴力枚举的方法求解出正确的明文简直是小菜一碟。如果选择使用统计分析法,破解的速度应该会更快。
但对于普通置换密码和乘法密码相比之下,已经有了很大的改进与提高。
多表代换密码
多表代换密码打破了原语言的字符出现规律,故其分析比单表代换密码的分析要复杂得多。
维吉尼亚密码是多表代换密码得经典代表,此处以维吉尼亚密码分析为例。
多表代换密码体制得分析方法主要分为3步
1 | 确定密钥长度(常用方法:卡希斯基测试法和重合指数法); |
为了方便,我还把密文中的非字母去掉了
1 | def cleanunalpha(cipher): |
确定密钥长度
现在进行第一步确定密钥长度,这里使用重合指数法
指数重合法利用随即文本和英文文本的统计概率差别来分析密钥长度。
假设某种语言由n个字母组成,每个字母i发生的概率为pi,1≤i≤n , 则重合指数就是指两个随机字母相同的概率:
$$
IC=\sum_{i=1}^{n}{p_i^2}
$$
值得注意的是,在单表代换的情况下, 明文与密文的IC值是相同的。
由于在现实世界中密文的长度有限,一般采用IC的无偏估计值来近似计算IC。
$$
IC′=\sum_{i=1}^{n}{\frac{x_i(x_i−1)}{L(L−1)}}
$$
其中xi表示密文符号i出现的次数,L表示密文长度,n表示某门语言包含的字母数,如该语言是英文字母,则n=26。
1 | def length(cipher): |
确定密钥
第二步使用拟重合指数测试法确定密钥。
设某种语言由n个字母组成,每个字母i在第一个分布中发生的概率为ri,在第二个分布中发生的概率为qi,则拟重合指数定义为
$$
x=\sum_{i=1}^{n}r_iq_i
$$
1 | # 使用重合指数法确定秘钥内容:遍历重合指数的最大值为标志 |
恢复明文
最后恢复明文,使用维吉尼亚解密
1 | def VigenereDecrypt(cipher,key): |
运行结果

安全性分析
维吉尼亚密码属于多表代换密码,多表代换密码打破了原语言的字符出现规律,故其分析比单表代换密码的分析要复杂得多。维吉尼亚加密的密钥空间大小为26m,对于一个相对小的m穷举也需要很长时间。
相较于单表代换,多表代换的安全性有了显著提高,需要猜测更多的字母表,并且频率分布特性也变得平坦。但多表代换密码也可以使用统计分析法破解,使用统计方法破解多表代换密码的前提是拦截到足够多的密文,这样才具备了统计分析的前提,所以对于传输量较小的明文加密,可以选择多表代换,比较安全。
序列密码
密钥序列
序列密码强度完全依赖于密钥序列的随机性和不可预测性。
密钥序列有需要具备以下功能:周期极大,均匀的n元分布,均匀的游程分布,良好的混乱性和扩散性。
由线性反馈移位寄存器所产生的序列中,像m序列具有良好的伪随机性,但它的密码强度很低,不过它的实现简单、速度快、由较为成熟的理论依据这些优点,现在在通信等工程技术中还是有广泛的应用。
线性反馈移位寄存器
选择一个15次以上的不可约多项式,编写一个线性反馈移位寄存器。验证生成序列的周期。
LFSR图示如下
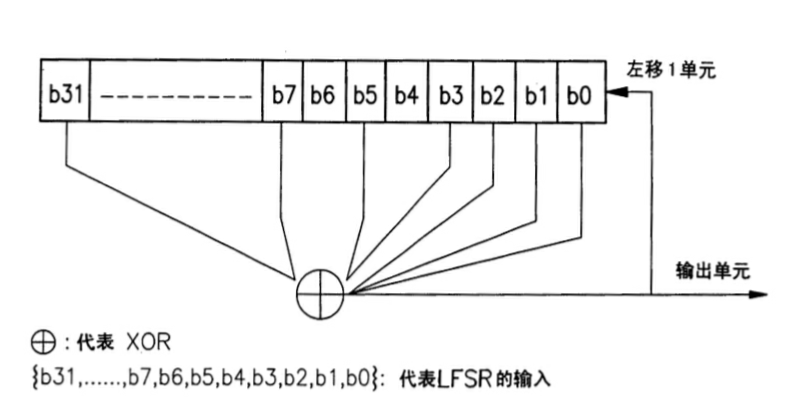
附上百度百科本原多项式词条中常用本原多项式

此处选择了n=16的本原多项式
$$
x^{16}+x^{12}+x^3+x+1
$$
验证生成序列的周期即验证n级LFSR的输出序列在重复之前能够参产生2n-1位长的伪随机序列(除去全0的情况)。
1 | s=input() |
运行结果
验证周期

寄存器状态
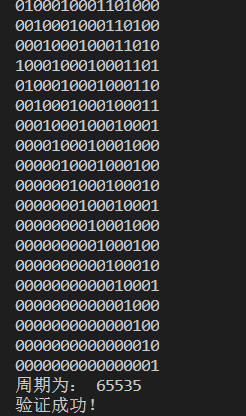
此处只截取了最后几个状态,一共有65535个状态
LFSR周期分析
为了使LFSR生成最大周期序列,其生成多项式必须为本原多项式,当其阶为n时,应产生2n-1位长的伪随机序列。同时初态对输出序列的周期没有影响,其周期取决于LFSR所使用的反馈函数。
RC4
RC4是一个典型的基于非线性数组变换的序列密码。它以一个足够大的数组为基础,对其进行非线性变换,产生密钥序列,一般把这个大数组称为S盒。
RC4包含两个处理过程:
1 | 密钥调度算法KSA,用来置乱S盒的初始排列 |
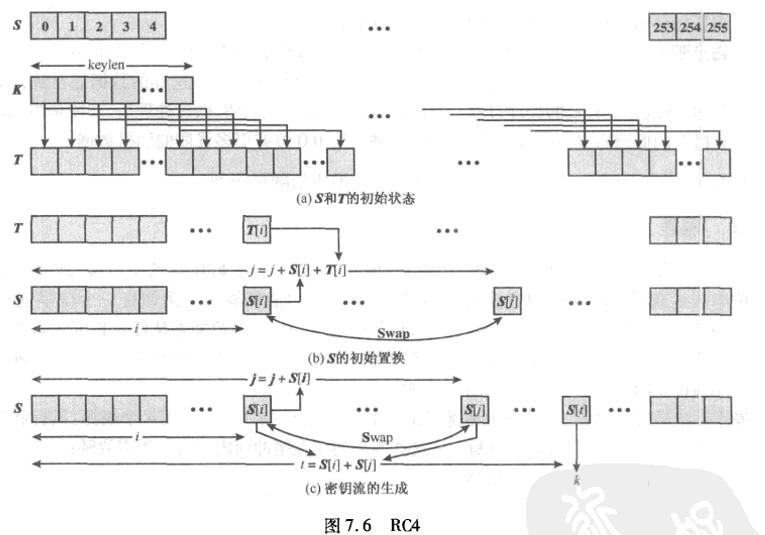
KSA
KSA首先初始化S,即S[i]=i(i=0~255),同时建立一个临时数组向量T(|T|=256),如果种子密钥K的长度为256字节,则直接将K赋给T,否则,若种子密钥K的长度小于|T|,则将K的值赋给T的前|K|个元素,并不断重复加载K的值,直到T被填满。
1 | lk = len(key) |
用T产生S的初始置换,从S[0]到S[255],对每个S[i],根据T[i]的值将S[i]与S中的另一个字节对换。
1 | j = 0 |
PRGA
从S中随机选取一个元素输出,并置换S以便下一次选取,选取过程取决于索引i和j,最后加解密都是将k与明文或密文字节异或。
1 | i = j = 0 |
最后用base64编码一下就okk了。
运行结果
加密

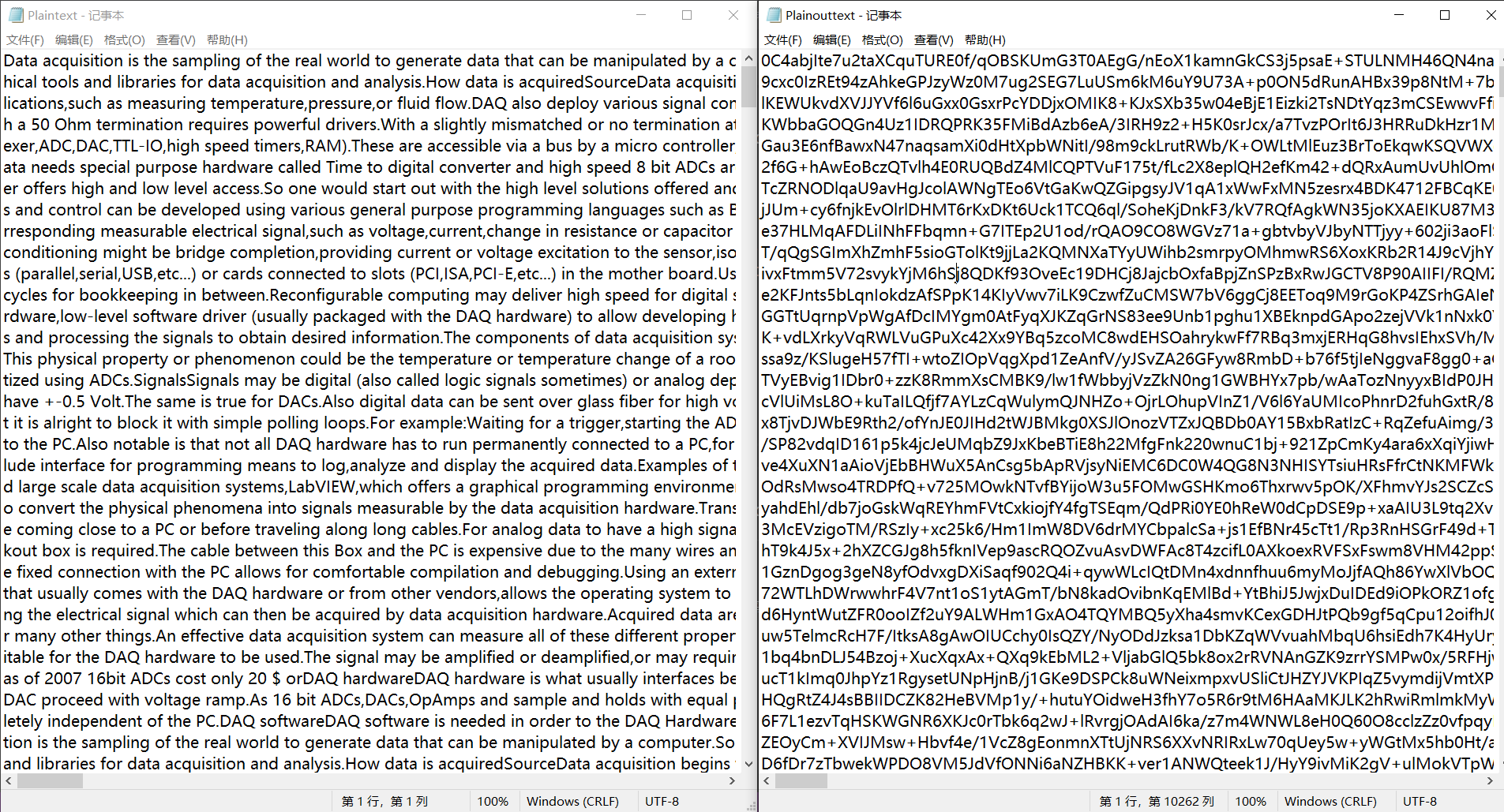
左边为明文,右边为加密后的密文
解密

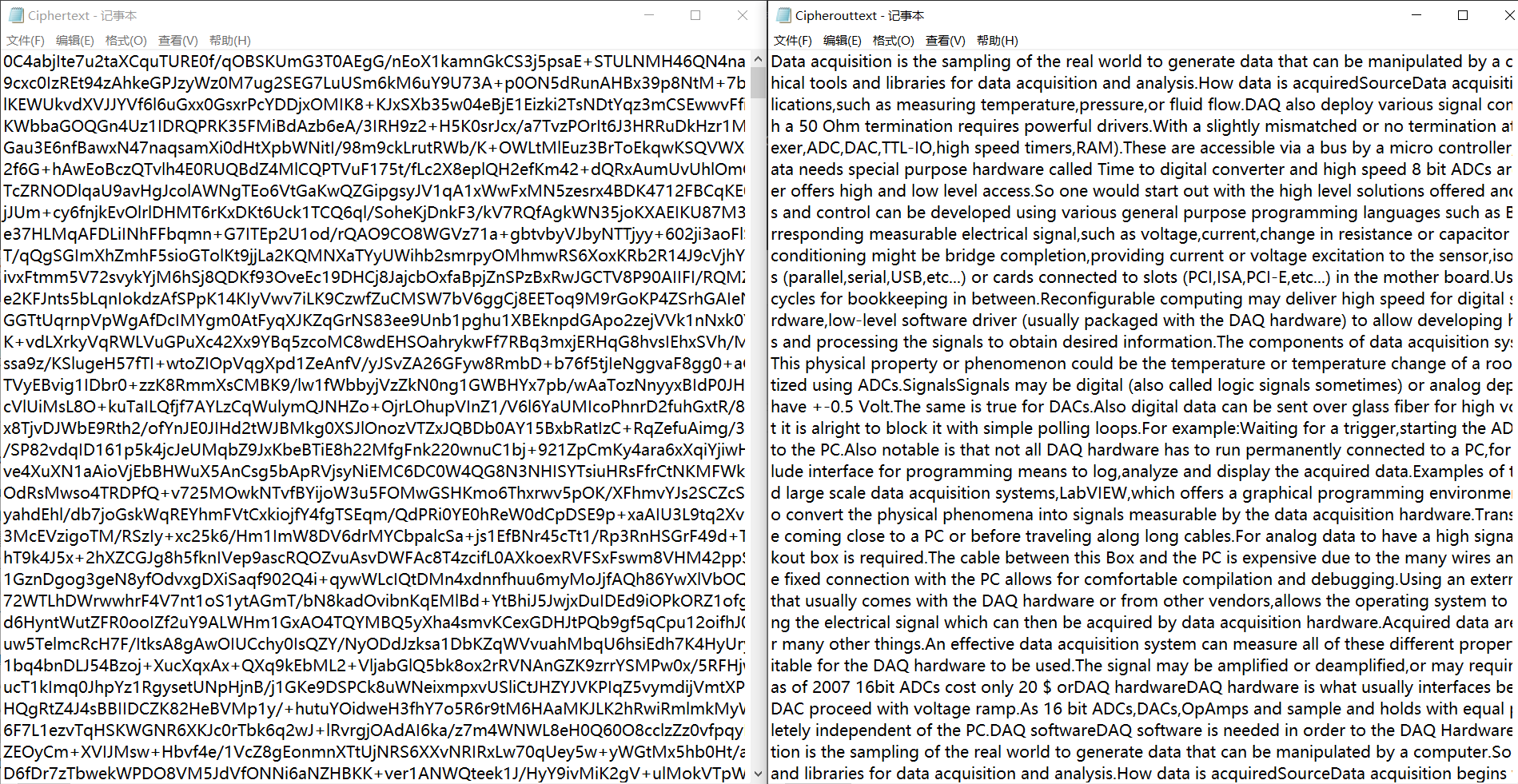
左边为密文,右边为解密后的明文
RC4安全性分析
RC4 算法容易用软件实现,加解密速度快(大约是 DES 的10倍)。
需要特别注意的是,为保证安全强度,目前的 RC4 至少要求使用 128 位密钥。
RC4 算法可看成一个有限状态自动机,大约有 21700种可能的状态。
分组密码
分组密码(block cipher)的数学模型是将明文消息编码表示后的数字(简称明文数字)序列,划分成长度为n的组(可看成长度为n的矢量),每组分别在密钥的控制下变换成等长的输出数字(简称密文数字)序列。
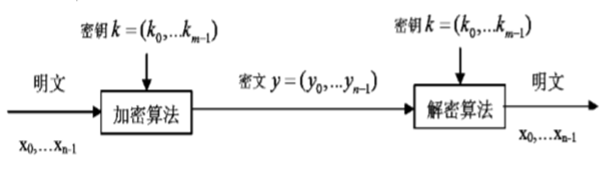
DES
基本结构
DES是一个对称密码体制,加密和解密使用同一密钥,有效密钥的长度为56位。DES是一个分组密码算法,分组长度为64位,即对数据进行加密和解密的单位是64位,明文和密文的长度相同。另外,DES使用Feistel结构,具有加解密相似特征。
基本原则
DES设计中使用了分组密码设计的两个原则:混淆(confusion)和扩散(diffusion),其目的是抗击敌手对密码系统的统计分析。
混淆是使密文的统计特性与密钥的取值之间的关系尽可能复杂化,以使密钥和明文以及密文之间的依赖性对密码分析者来说是无法利用的。
扩散的作用就是将每一位明文的影响尽可能迅速地作用到较多的输出密文位中,以便在大量的密文中消除明文的统计结构,并且使每一位密钥的影响尽可能迅速地扩展到较多的密文位中,以防对密钥进行逐段破译。
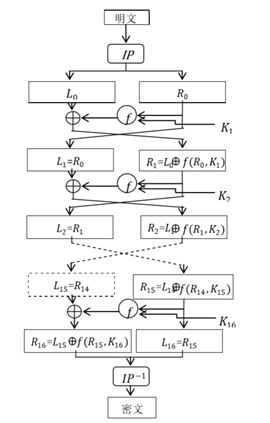
算法步骤
以上图DES加密为例,解密为逆过程。
1 | 64的明文经过初始置换(IP)而被重新排列,并将其分为左右两个分组L0和R0,各为32位。 |
加密过程
$$
L_0R_0{\leftarrow}IP(<64位明文>)
$$
$$
L_i{\leftarrow}R_{i-1}
$$
$$
R_i{\leftarrow}L_{i-1}{\bigoplus}F(R_{i-1},K_i)
$$
$$
L_{16}{\leftarrow}L_{15}{\bigoplus}F(R_{15},K_{16})
$$
$$
R_{16}{\leftarrow}R_{15}
$$
$$
<64位密文>{\leftarrow}IP^{-1}(L_{16}R_{16})
$$
解密过程
$$
L_{16}R_{16}{\leftarrow}IP(<64位密文>)
$$
$$
R_{i-1}{\leftarrow}L_{i}{\bigoplus}F(R_{i},K_i)
$$
$$
L_{i-1}{\leftarrow}R_i
$$
$$
L_{0}{\leftarrow}L_{1}{\bigoplus}F(R_{1},K_{1})
$$
$$
R_{0}{\leftarrow}R_{1}
$$
$$
<64位明文>{\leftarrow}IP^{-1}(L_{0}R_{0})
$$
算法实现
1 | #字符串转化为二进制 |
密钥编排
DES的最初64位密钥通过置换选择PC-1得到有效的56位密钥。
经过循环左移和置换选择2 ( PC-2 ) 后分别得到 16 个 48 位子密钥 Ki 用做每一轮的迭代运算。
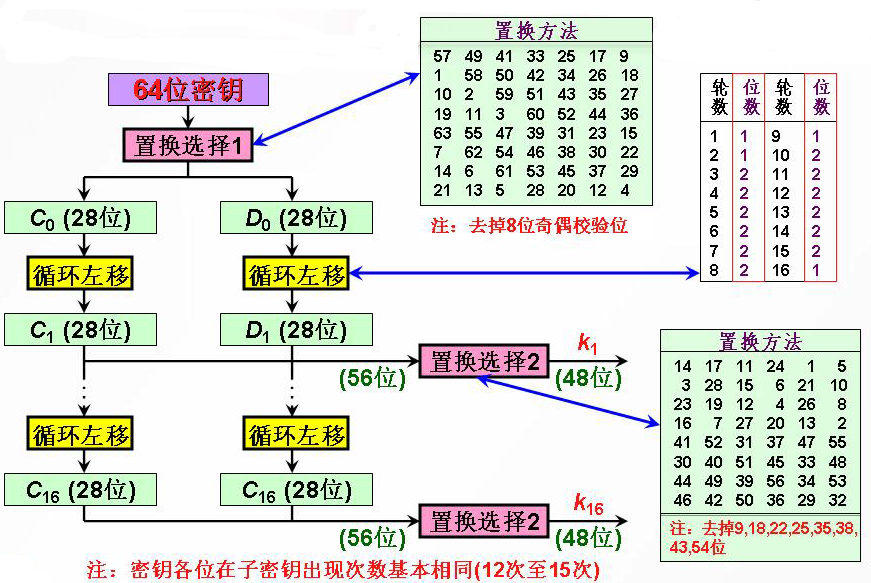
置换选择
1 | #密钥的PC-1置换 |
密钥生成
1 | def gen_key(key): |
循环左移
1 | #循环左移操作 |
初始置换和逆初始置换
初始置换(IP)是在第一轮迭代之前进行的,目的是将原明文块的位进行换位,其置换表是固定的。逆初始置换(IP-1)是初始置换的逆置换。
IP 最后一列为 2, 4, 6, 8, 1, 3, 5, 7,左一列比右一列+8 。
IP-1 第二列为 8, 7, 6, 5, 4, 3, 2, 1,右边第二列比当前列+8 。
初始置换
1 | #IP盒处理 |
轮函数F
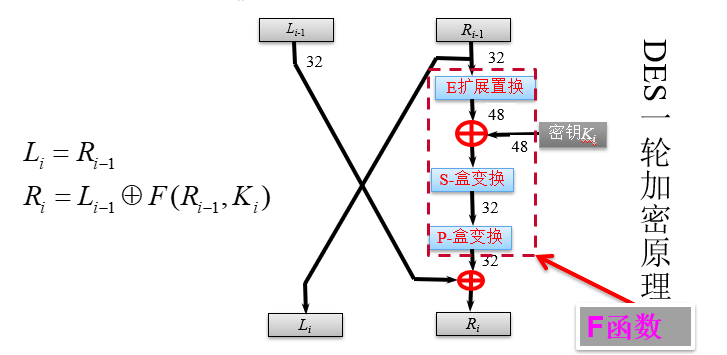
DES轮函数F由4部分组成
1 | 扩展置换(E盒) |
扩展置换
扩展置换又称E盒,它将32位输入扩展为48位输出。
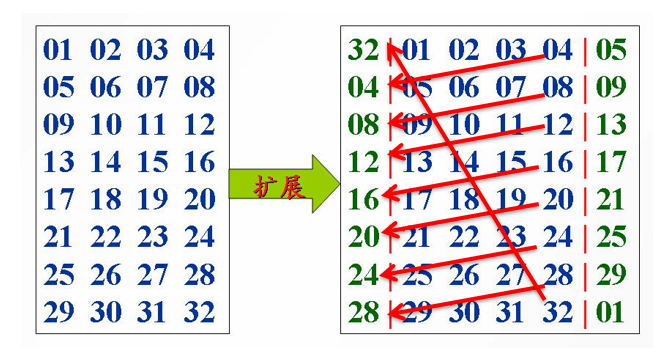
扩展方法:每个输入分组的4位作为6位输出分组的中间4位,6位输出分组中的第1、6位分别由相邻两个4位分组的最外面两位扩散进入到本分组,其中第1个分组的左侧相邻分组为最后1个分组。

扩展置换的目的
1 | E盒产生于子密钥相同长度的数据使得能进行异或运算 |
1 | #E盒置换表 |
密钥加
E扩展输出的48位数据与48位子密钥进行逐位异或运算,输出48位数据。
1 | #字符串异或操作 |
这里变成10进制是转化成字符串,2进制与10进制异或结果一样,都是1,0。
代换盒
代换盒又称作S盒,其功能是进行非线性代换。
S盒是DES中唯一的非线性部分,经过S盒代换以后,E盒扩展生成的48位数据又重新被压缩成32位数据。
压缩替换S-盒由8个S-盒构成, 每个S-盒都是6比特的输入,4比特的输出。
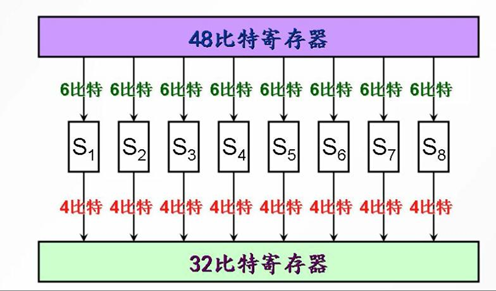
S盒的构造
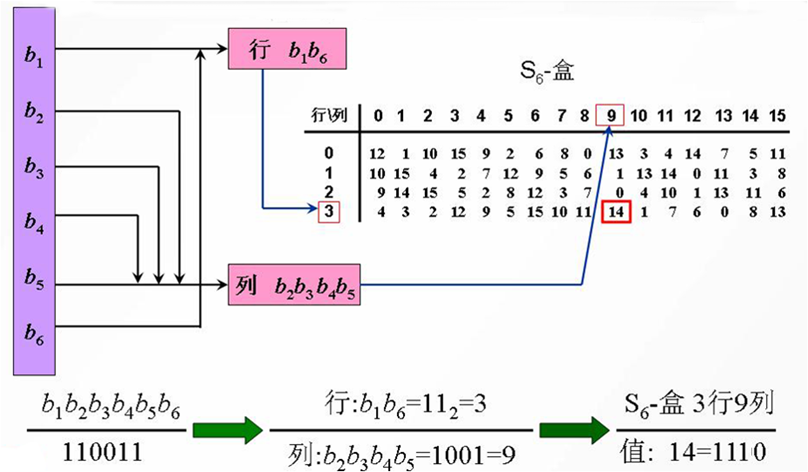
S盒设计准则
1 | 具有良好的非线性(输出的每个比特与全部输入比特有关) |
1 | def s_box(my_str): |
置换运算
置换运算(P盒)只是进行简单位置置换。
1 | #P盒置换表 |
F函数实现
1 | def fun_f(bin_str,key): |
加解密算法
加密代码
1 | def des_encrypt_one(bin_message,bin_key): #64位二进制加密的测试 |
解密代码
1 | ##64位二进制解密的测试,注意密钥反过来了,不要写错了 |
填充密钥
全部密钥以补0的方式实现长度不满足64位的。
1 | #简单判断以及处理信息分组 |
密钥超过64位的情况默认就是应该跟密文一样长直接将密钥变为跟明文一样的长度,虽然安全性会有所下降。
运行结果
加密
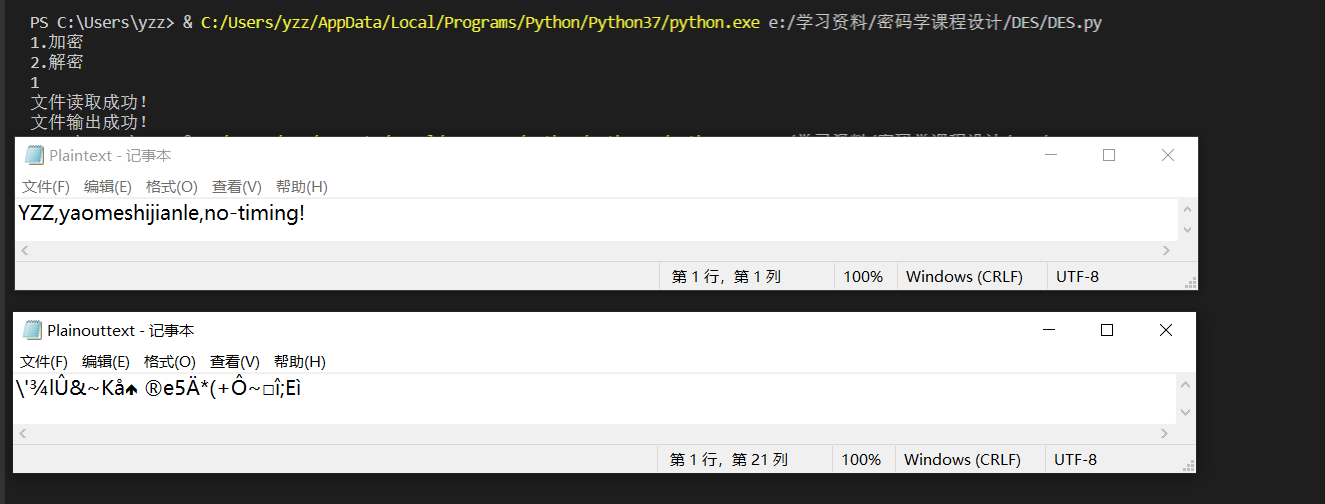
上边为明文,下边为加密后的密文
解密
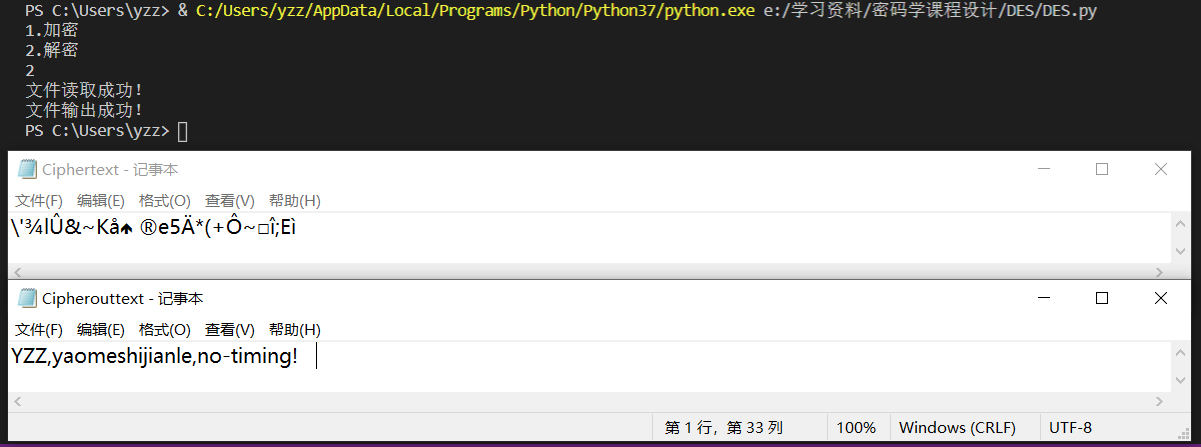
上边为密文,下边为解密后的明文
安全性分析
互补性
若
$$
c=E_k(m)
$$
则有
$$
\overline{c}=E_{\overline{k}}(\overline{m})
$$
在选择明文攻击下所需的工作量减半,仅需要测试256个密钥的一半就可以破解。弱密钥
对于加密解密运算没有区别的密钥叫弱密钥。如果k为弱密钥,则对于任意的64位数据m,有
$$
E_k(E_k(m))=m
$$
和
$$
D_k(D_k(m))=m
$$
有弱密钥产生是因为C、D存储的数据在循环移位时除位置外没有发生变化(C、D全为0或全为1)。此外还有半弱密钥,四分之一弱密钥和八分之一弱密钥,共256个。
如果随机选取密钥,选中弱密钥的概率几乎可以忽略,但一般为了安全起见,在随机生成密钥后,要进行弱密钥检查,以保证不使用弱密钥作为DES的密钥。
迭代轮数
对于低于16轮的DES已知明文攻击,差分分析攻击比穷举攻击有效。
当DES进行到16轮迭代时,穷举攻击比差分分析攻击有效。密钥长度
DES密钥长度为56位,按照当时的计算能力,对于这个长度的密钥进行穷举攻击是不切实际的,但现在已经成为了现实。
改进
人们针对DES设计了改进方法:多重DES。
多重DES就是使用多个不同的DES密钥利用DES加密算法对明文进行多次加密。使用多重DES可以增加密钥量,从而大大提高抵抗对密钥的穷举搜索攻击的能力。
- 双重DES
可以抵抗目前的穷举攻击,但无法抵抗中途相遇攻击,即获得一对明密文,使得一起从双方各自的起点出发,一段进行加密,另一端进行解密,当找到两端相同的时候,二重DES就被破解了。
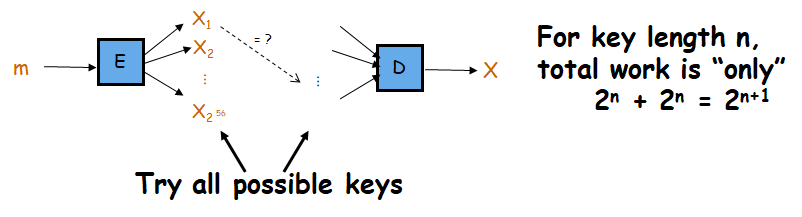
- 三重DES
1 | 密钥长度增加到112位或168位 |
因此三重DES知识在DES变得不安全的情况下的一种临时解决方案。
公钥密码
公钥密码 又称为非对称密码,拥有公钥密码的用户分别拥有加密密钥和解密密钥。通过加密密钥不能得到解密密钥。并且加密密钥是公开的。
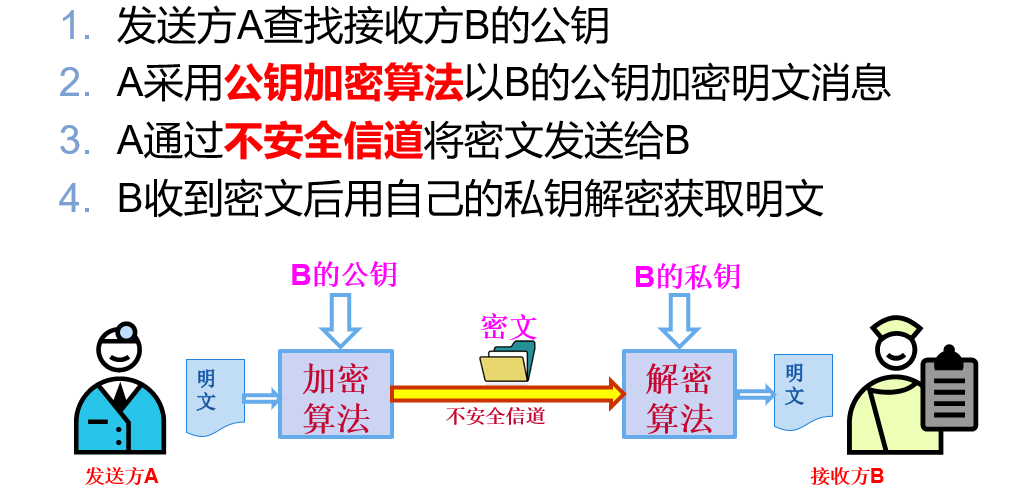
RSA
该算法的数学基础是初等数论中的欧拉定理。
其安全性基于大整数因子分解的困难性。
算法描述
密钥的生成
选择两个大素数 𝑝和𝑞,(𝑝≠𝑞,需要保密,步骤4以后建议销毁)
计算
$$
n=p×q,\varphi(n)=(p-1)×(q-1)
$$选择整数e使
$$
(\varphi(n),e)=1,1<e<\varphi(n)
$$计算d,使
$$
d=e^{-1}mod\varphi(n)
$$
得到:公钥为{e,n};私钥为{d}
加密(用e,n):明文M<n,密文
$$
C=M^e(modn)
$$解密(用d,n):密文C,明文
$$
M=C^d(modn)
$$
密钥的生成
这一步是整个RSA最重要的一步,其安全性就是基于大整数因子分解的困难,所以,选择两个大素数p和q就显得尤为重要!!!
那么,怎么选择呢?
一般的,选取一个素数的过程如下
1 | 随机选一个奇数𝑛(如使用伪随机数产生器) |
Miller-Rabin素数测试算法
费马小定理
设p是一个素数,则对任意整数a,有
$$
a^p{\equiv}a(modp)
$$
二次探测如果p是一个素数,0<x<p,则方程
$$
x^2{\equiv}1(modp)
$$
的解为
$$
x=1或x=p-1
$$
要测试N是否为素数,首先将N−1分解为2sd。在每次测试开始时,先随机选一个介于[1,N−1]的整数a,之后如果对所有的r∈[0,s−1],若ad mod N ≠ 1且a2rd mod N ≠ −1,则N是合数;否则,N有3/4的概率为素数。
增加测试的次数,该数是素数的概率会越来越高。
具体操作:先用randrange()函数生成一个大伪随机数,然后再用Miller-Rabin素数测试算法判断它是不是素数,若是则就用它;不是则再随机生成一个新的伪随机数,再判断,直到找到可以用的大伪随机数p和q。
1 | #Miller_Rabin算法 |
模重复平方计算法
快速求幂运算
1 | def fast_mod(b,n,m): |
公钥e的选择
$$
(\varphi(n),e)=1,1<e<\varphi(n)
$$
在RSA算法中,e和(p-1)*(q-1)互质的条件容易满足,如果选择较小的e,则加、解密的速度加快,也便于存储,但会导致安全问题。
为了减少加密运算时间,很多人采用尽可能小的e值,如3。但是已经证明低指数将会导致安全问题,故此,一般选择e为16位的素数,可以有效防止攻击,又有较快速度。
1 | def E(fn): |
计算私钥d
$$
d=e^{-1}mod\varphi(n)
$$
这里使用扩展欧几里得法求逆元
1 | def D(e,fn): |
加解密算法
加密
$$
C=M^e(modn)
$$
1 | def RSA_encrypt(e,n,plaintext): |
解密
$$
M=C^d(modn)
$$
1 | def RSA_decrypt(d,n,ciphertext): |
运行结果
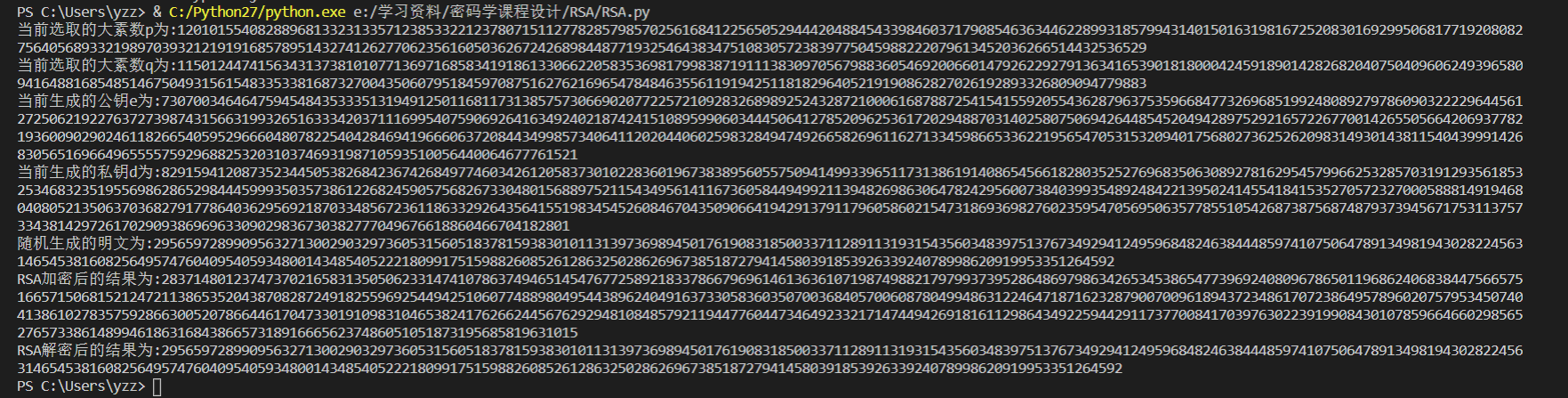
效率分析
由于RSA 的核心算法是模幂运算(大数自乘取模),要提高RSA 算法的效率,首要问题是提高模幂运算的效率。为了找到模幂运算的优化方法,我们不妨先来分析一般的模乘运算(两大数相乘取模),模乘过程中复杂度最高的环节是取模运算,因为一次除法实际上包含了多次加法、减法和乘法,如果在算法中能够尽量减少除法甚至避免除法,则算法的效率会大大提高。
安全性分析
因子分解法
RSA密码体制的安全性主要依赖于整数因子分解问题,试图分解模数n的素因子是攻击RSA最直接的方法。分解方法有试除法、 p−1因子分解法、p+1因子分解法、二次筛因子分解法、椭圆曲线因子分解法、数域筛因子分解法等。但由于因子分解的时间复杂性并没有降为多项式时间,因此,因子分解还是一个计算上的难题,只是需要考虑使用较大的位数,以确保无法在短时间内被破解。
针对参数选择的攻击
共模攻击
多个用户使用相同的模数n,但公、私钥对不同。这种做法是不安全的。同样,不同用户选用的素因子p和q不能相同,因为n是公开的,如果素因子相同,可通过求模数n的公约数的方法得到相同素因子,从而分解模数n。
低指数攻击
为了增强加密的高效性,希望选择较小的加密密钥e。如果相同的消息要送给多个实体,就不应该使用小的加密密钥。同样的,加密密钥d也不能取得太小。
p-1和q-1都应有大的素数因子
攻击防范措施
密钥长度
密钥长度使用至少1024位,现在大部分使用1024*3位
参数选择
- 为避免椭圆曲线因子分解法,p和q的长度相差不能太大
- p和q的差值不应该太小
- gcd(p-1,q-1)应尽量小
- p和q应为强素数
Hash函数
Hash,一般翻译做散列、杂凑,或音译为哈希,是把任意长度的输入(又叫做预映射pre-image)通过散列算法变换成固定长度的输出,该输出就是散列值。这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,不同的输入可能会散列成相同的输出,所以不可能从散列值来确定唯一的输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。
MD5
算法描述
MD5算法的输入是长度小于264比特的消息,输出为128比特的消息摘要。输入消息以512比特的分组为单位处理,流程图如下
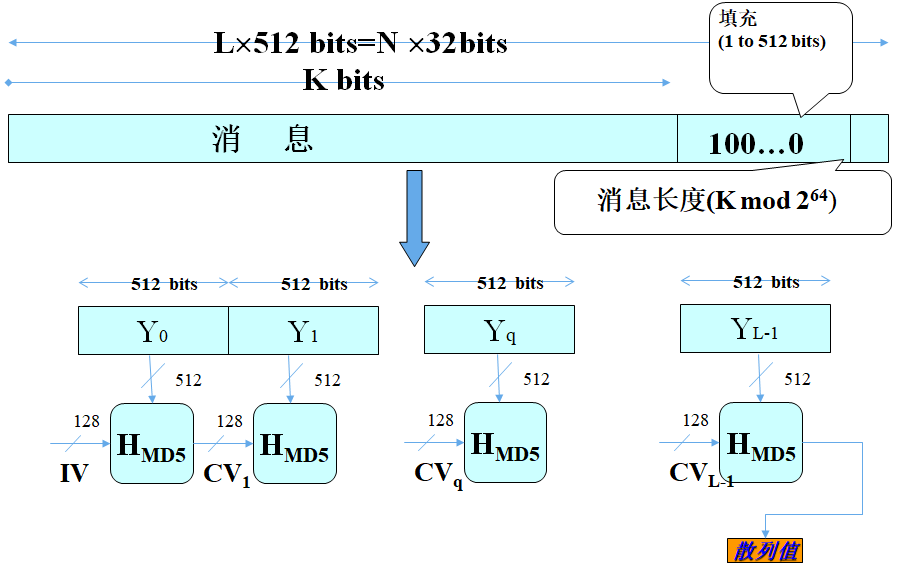
具体过程
附加填充位
使消息长度模512=448,如果消息长度模512恰等于448,增加512个填充比特。即填充的个数为1~512。
需要特别注意的是,若原始消息长度刚好满足模 512 与 448 同余,则还需要填充 1 个 1 和 511 个 0 。
填充方法:第1比特为1,其余全部为0
补足长度
将消息长度转换为64比特的数值。
如果长度超过64比特所能表示的数据长度,值保留最后64比特。
添加到填充数据后面,使数据为512比特的整数倍。
512比特按32比特分为16组。
64比特消息长度
先将消息长度写成 64 bit ,长度不足64位消息自行填充,然后变换成小端序
1 | length = Little_endian(bin(lm%(2**64))[2:].zfill(64),False) |
初始化链接变量
MD5使用4个32位的寄存器A,B,C和D,最开始存放4个固定的32位的整数参数,即初始链接变量。
1 | a,b,c,d= (0x67452301, 0xefcdab89, 0x98badcfe, 0x10325476)#小端序 |

这里为了方便,可以将小端序封装成一个函数,用来将二进制或十六进制组成的字符串转成小端序
1 | def Little_endian(s,Hex): |
分组处理
由4轮组成,512比特的消息分组Mi被均分为16个子分组参与每轮16步函数运算。
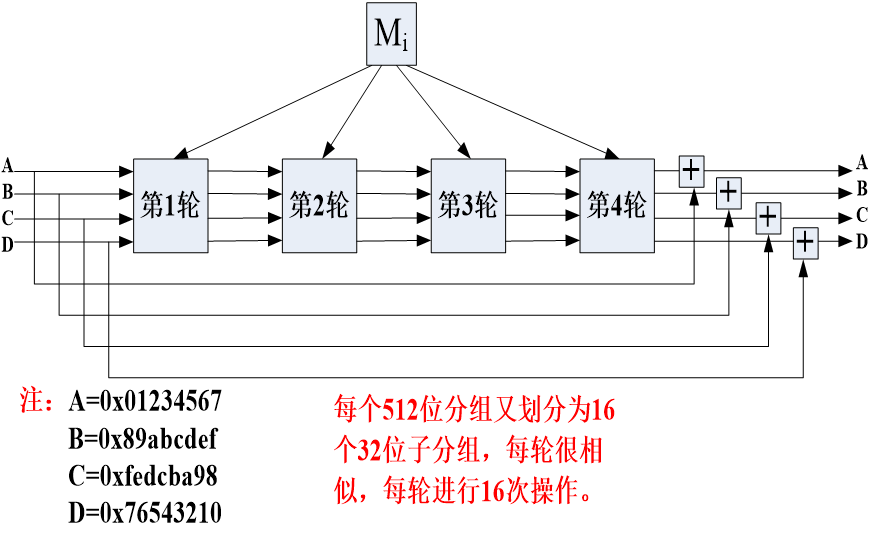
步函数
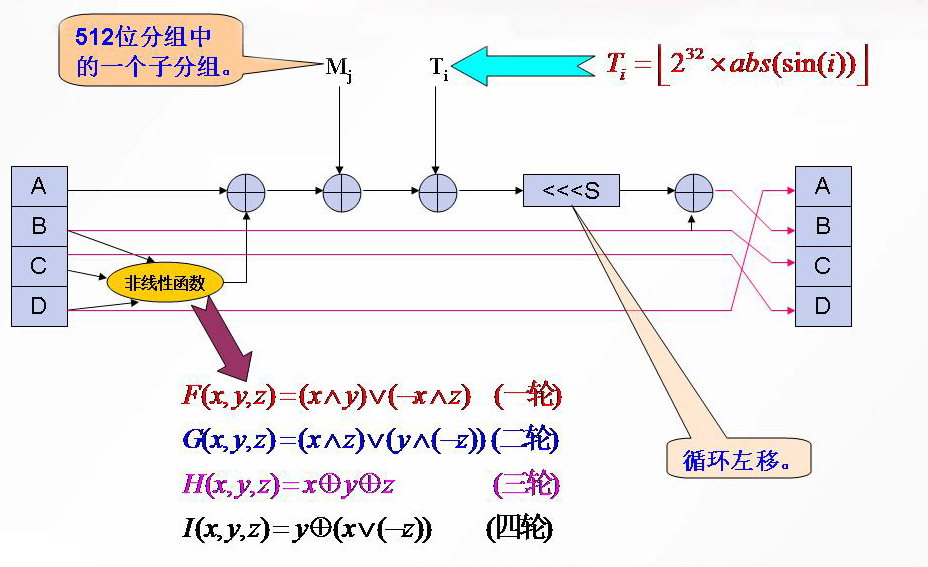
上一步的D,B,C直接赋给下一步的A,C,D,而上一步的A需要进行变换赋给B。
这里的加法都是模232加法,为了方便起见,封装封装!!!
1 | def mod32(a,b): |
A先与分线性函数变换结果相加,再和M[j]相加,再与T[i]想加,循环左移s位,最后于原来的B相加,得到新的B。
非线性函数
见上图
使用lambda表达式来写
1 | F = lambda x,y,z:((x&y)|((~x)&z)) |
M[j]
表示消息分组Mi的第j(0≤j≤15)个32比特子分组。
第一轮以字的初始次序使用
后面三轮的次序由下面置换确定
$$
P_2(i)=(1+5i)mod16
$$
$$
P_3(i)=(5+3i)mod16
$$
$$
P_4(i)=7imod16
$$
在程序中我们直接打表
1 | #每次 M[i]次序。 |
T[i]
常数 T[i]为
$$
2^{32}×abs(sin(i))=[4294967296×abs(sin(i))]
$$
其中i为弧度(1≤i≤64)
循环左移
打表
1 | L = lambda x,n:(((x<<n)|(x>>(32-n)))&(0xffffffff)) |
输出
如果所有512分组操作完毕,输出
$$
A‖B‖C‖D
$$
即为消息的MD5值(消息摘要)
运行结果
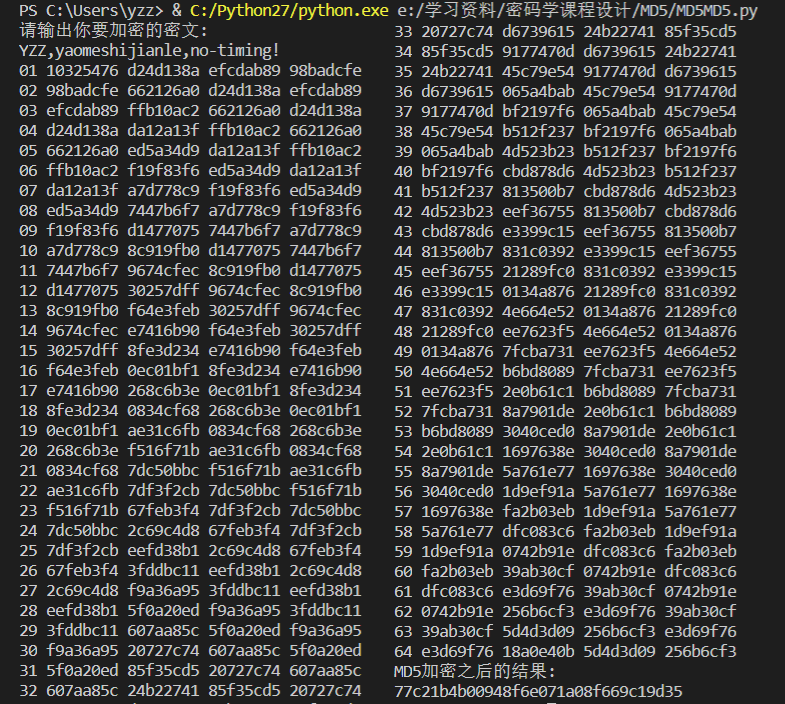
将该程序MD5加密后的结果与网络在线MD5加密的结果做对比
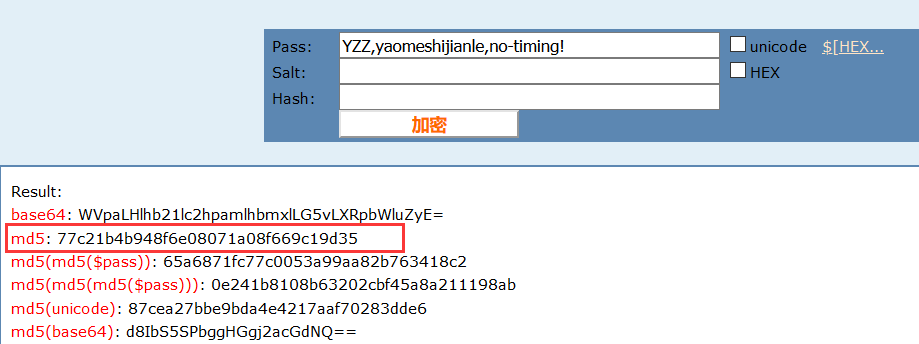
二者完全一致!
效率分析
MD5由MD4改进而来,但MD5的速度较MD4降低了近30%,在一般配置的PC机上使用MD5算法,处理1G的文件数据只需20-30秒(有些专用设备声称达 3GB/秒),不会对应用或机器带来过多负载,相对其他的哈希函数,其效率较好。
安全性分析
Hash函数是将任意长度消息压缩成固定长度的”消息摘要“,所以它是一个多对一的函数,故必然存在”碰撞“,虽然概率很小。
从单向性考虑,虽然Hash函数是不可逆的,但是仍然可以使用某些方法从像推出原像,同时现在也有很多在线MD5解密网站。
Hash函数普遍容易遭受长度扩展攻击,就是在已知输入明文的长度和其 MD5 值的情况下,可以在明文后面附加任意内容,同时能够推算出新的正确的 MD5。
综合实验
Alice想要通过公共信道给Bob传输一份秘密文件(文件很大),又知道,很多人和机构想得到这份文件。如果你是Alice,你应该怎么做?请设计一个方案,并编程实现。
思路
审题:
首先注意到秘密文件很大,这时候就需要比较各种加密算法的效率。
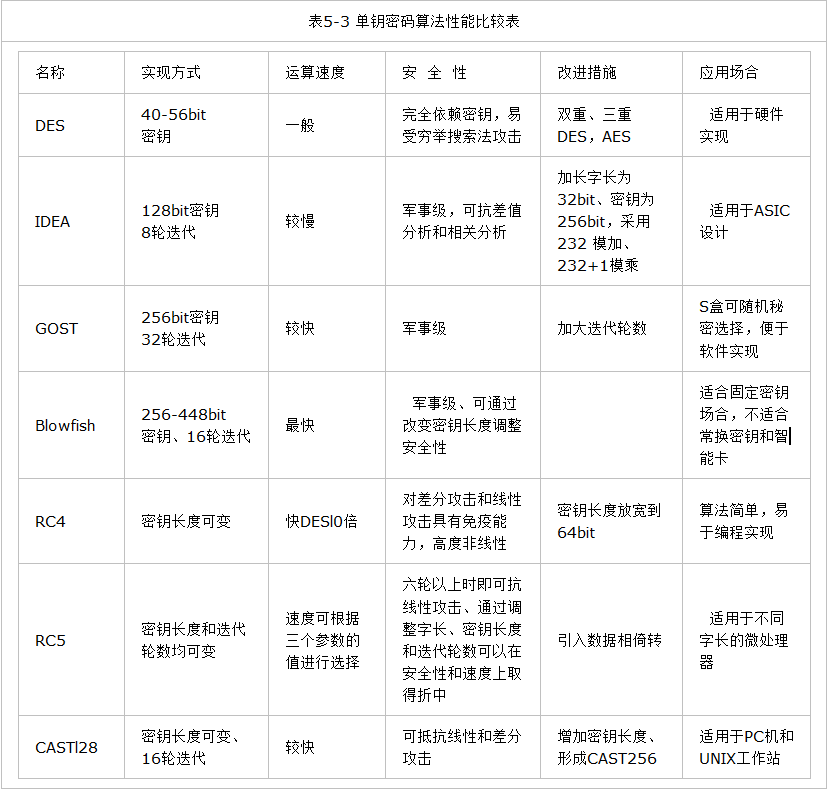
我只写了DES和RC4,所以就是比较DES和RC4的运算速度,看表可以看出,RC4的速度比DES快10倍,那就选RC4对秘密文件进行加密。
RC4属于对称密码,对称密码的密钥分发是需要通过安全信道,题目说“很多人和机构都想得到这份文件”,说明,这个信道肯定是不安全的,所以我们需要对分发的密钥进行加密传输,这个时候使用公钥密码体制对密钥进行加密。
公钥密码体制选择RSA
流程
大致流程就是
1 | Alice随机生成两个大素数p和q,计算出RSA的公钥{e,n},私钥{d,n} |
生成密钥
先用RSA随机生成两个大素数p和q。
1 | p=create_prime() |
计算公钥{e,n},私钥{d,n}。
1 | n=p*q |
Bob选取RC4密钥k进行RSA加密
1 | k = "LGDISTHEBEST" |
Alice解密密钥k
1 | k2=RSA_decrypt(d,n,int(k1)) |
Alice使用k对文件进行RC4加密
1 | RC4Encrypt(c1,q) |
Bob使用k对文件解密
1 | RC4Decrypt(message,k) |
注意事项
这个程序改了好久,对RC4密钥k加密解密那里卡了好久!
一开始,我想到是字符串k转成二进制,然后直接用RSA加解密,但是一想不对呀,这想法也太离谱了,一个二进制字符串也太大了!突然就想到可以先将二进制再转换成十进制,然后用RSA加密,传输的是加密得到的十进制数,解密的时候解出来是十进制,再转成二进制,最后转成字符串,就得到最初约定好的RC4密钥k!!!
也就是说
$$
字符串K{\Longrightarrow}二进制K{\Longrightarrow}十进制K{\Longrightarrow}RSA加密
$$
$$
RSA解密{\Longrightarrow}十进制K{\Longrightarrow}二进制K{\Longrightarrow}字符串K
$$
最后这个综合实验终于改完了!!!
运行结果
测试加密文件,其中c(10M)为一个10M的秘密文件

Alice和Bob进行通信
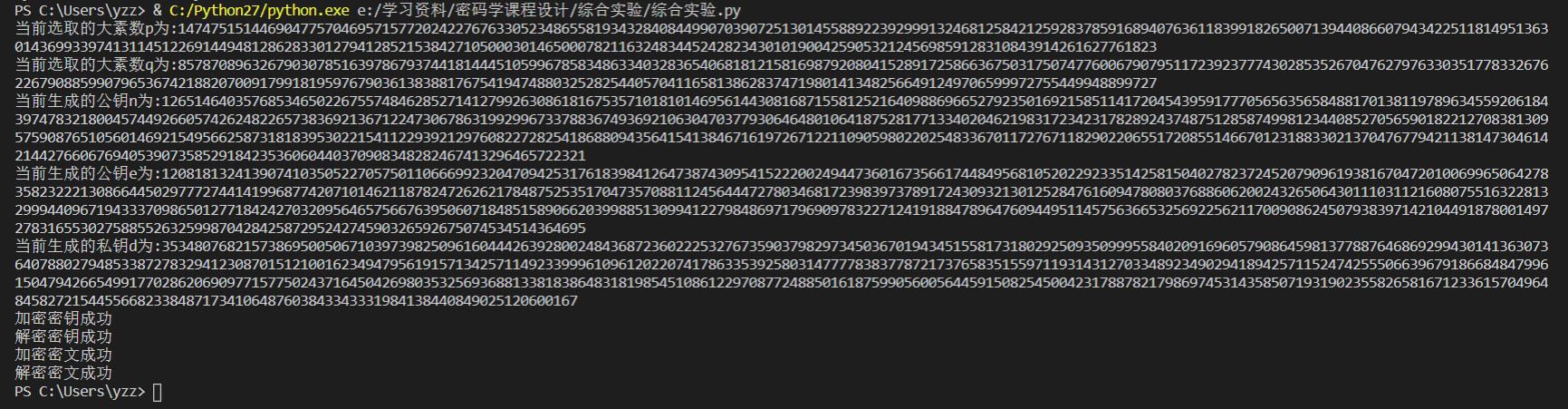
测试完各文件大小

各文件内容
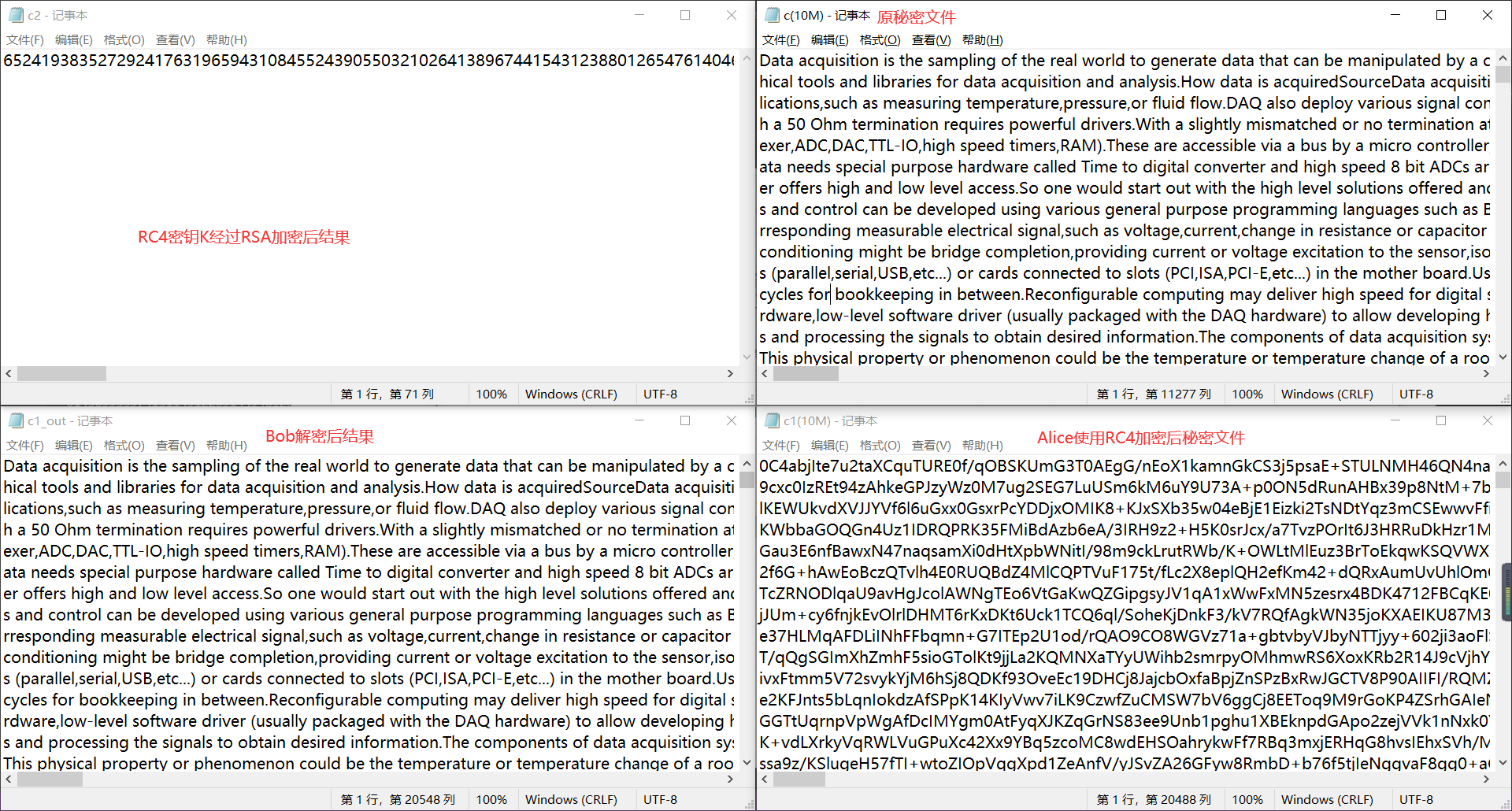
存在的问题
缺少身份认证机制
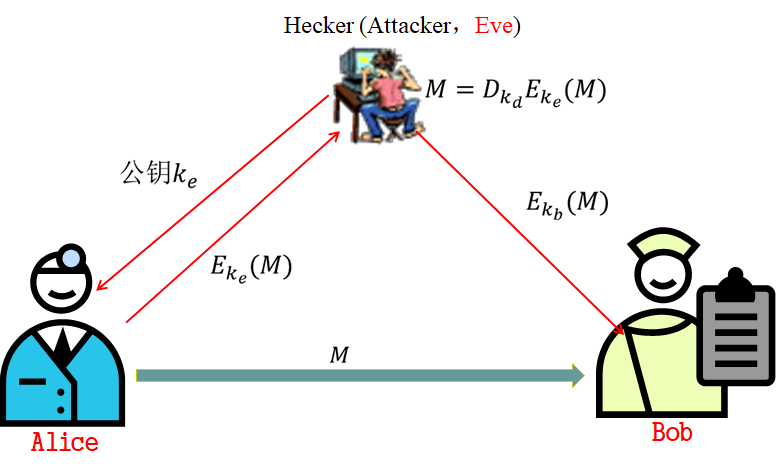
因为可能存在中间人 Eve ,Bob 首先要验证通信对方是不是 Alice,所以需要再写一个数字签名(保证消息的完整性、不可抵赖性)
基于RSA和MD5的数字签名
签名算法
对应RSA密码体制中的解密过程
设待签名的消息为m,则签名者A先利用一个安全的Hash函数 h 来产生一个消息摘要 h(m),然后签名者用自己的私钥计算签名 s ≡ h(m)d mod n ,将 (s,m) 发送给消息接收者 B。
1 | def Sign(m,d,n): |
验证算法
对应RSA密码体制中的加密过程
签名接收者B收到消息m和签名s后,先利用A使用的Hash函数h来产生一个消息摘要h(m),然后检验同余式 h(m) ≡ se mod n是否成立。若成立,则说明签名有效,否则签名无效。
1 | def Ver(m,s,n,e): |
注意点
验证算法中,求出消息Hash值以后,进行验证的时候要对n取模!!!
运行结果
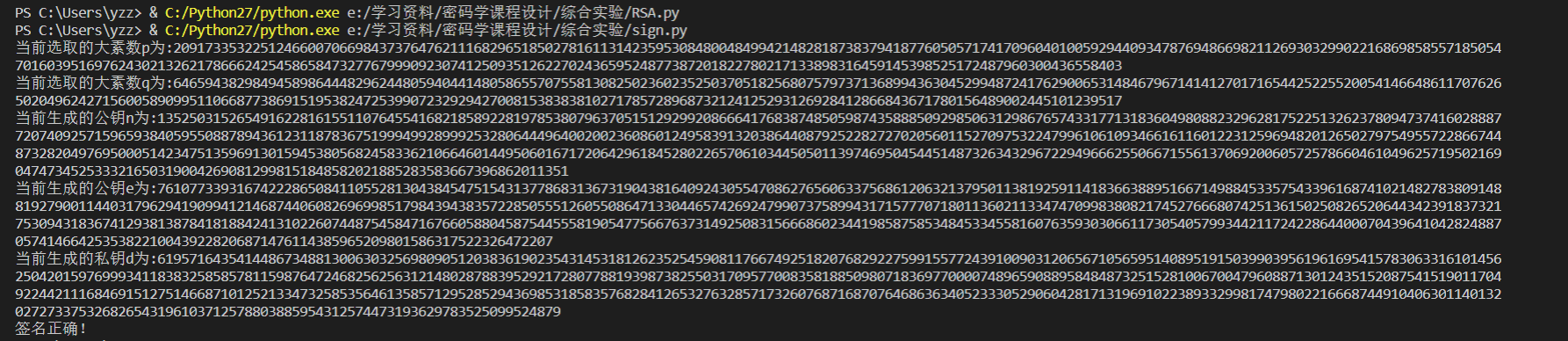
选择Python的原因
对比之前学习的编译型语言C++,作为解释型语言的Python在运行效率上自然完败,但对比二者的开发效率,Python可以说是完胜。Python的代码明了,思路清晰,语言更接近自然语言。Python一两句代码就搞定的东西,C++往往要写一大堆。最鲜明的例子就是对字符串的拼接操作了,Python只需要一个“+”就完成的操作,在C++里需要比较复杂的代码来完成。
Python有非常强大的第三方库,基本上想通过计算机实现任何功能,Python官方库里都有相应的模块进行支持,直接下载调用后,在基础库的基础上再进行开发,大大降低开发周期,避免重复造轮子。 尤其是对编码问题,通常情况下,加密后的密文并不是ASCII码范围内的字符或者不是可打印字符,而Python对base 64编码的操作十分简洁方便,但编码问题之后也给我挖了一个大坑。Python 2与Python 3的编码问题是我一开始编程没有想到的,之前的程序都是用Python 3写的,但 LSFR 之后,我发现自己遇到了编码的这个问题,同时发现Python 2的base 64更加方便简洁,于是之后的程序我都选择了Python 2来完成。对于Python 2和Python 3的编码转换问题,我也将继续学习,后续将尝试将Python 2的程序都转换成Python 3来重新完成。
这门课开始以前,我对于Python仅限于简单脚本的编写,数据结构和算法的程序都是使用C++完成,对于下学期要选修的Python课也是一个难得的提前预习的机会,当然不会放过。
心得体会
此次《密码学课程设计》持续4周,一周2次实验课,感觉自我收获还是很丰富的。众所周知,实践是检验真理的唯一标准,是否学好《密码学》的直接检验就是密码算法的编写成果。
我总共编写了10个程序,其中有仿射密码加解密、仿射密码的暴力破解与分析破解、多表代换的指数重合法、线性移位寄存器LFSR **、序列密码RC4、对称加密体制DES、公钥加密体制RSA、Hash函数消息摘要MD5、基于RSA和MD5的数字签名以及使用这些算法论述了如何实现一个通信保密的信息系统**。 同时也对这些加密算法通过效率、安全性等方面进行了分析,同时也针对某些密码体制进行了攻击的分析与实现。在实现对密码的攻击过程种能够更加熟悉密码体制的构建与实现。只有当你真正能够攻破它,你才完全掌握了它。
在此次编程实现密码算法的时候遇到了很多的困难,比如多表代换的指数重合法分析破解,在查阅了大量资料之后,才勉强做出来一个成果。在暴力破解和统计分析破解仿射密码的时候,有一个小小的遗憾,就是最后没有根据语言的语法来自动识别恢复的有效明文。之后又遇到了最大的麻烦,Python 2和Python 3的编码转换问题,当时我知道有这个问题的时候,都想全部重新用C++写了,但还好理性战胜了冲动,改用Python 2来编写之后的程序。在写MD5时遇到了小端序转换的难题以及消息长度填充的问题,在写综合实验的时候遇到了RC4密钥使用RSA加密的问题,具体问题归属于字符串转数字的问题,当时想了好久,才想到可以将字符串先转换成二进制,然后转换成十进制,之后用RSA加密。在基于RSA和MD5数字签名的算法中,验证算法中没有对H(m)取模之后再对比也卡了好久。总之,试一试总能出来的,就看自己坚持尝试了多少次。
21世纪是信息时代,信息的传递在人们日常生活中变得非常重要。信息交换中,“安全”是相对的,而“不安全”是绝对的,随着社会的发展和技术的进步,信息安全标准不断提升,因此信息安全问题永远是一个全新的问题。信息安全的核心是密码技术。如今,计算机网络环境下信息的保密性、完整性、可用性和抗抵赖性,都需要采用密码技术来解决。公钥密码在信息安全中担负起密钥协商、数字签名、消息认证等重要角色,已成为最核心的密码。这也是我们为何研究密码学的主要原因。
目前我国的密码技术提升速度很快,在国际上已经有举足轻重的地位。 国产的密码算法也绝对不比国际上的密码算法安全性差,同时推广也非常快。时至今日国内一半的计算机网络通信以现在的密码技术都能够提供保障。在祖国密码学发展蒸蒸日上的大环境下,我们这些选择信息安全专业的人也应当为之做出自己微薄的贡献。利用自己掌握的密码学知识为建立一个安全通信互联网尽自己的一份力量。
附录
仿射密码
加解密代码
1 | #辗转相除法 |
仿射密码暴力与分析解密代码
1 | def gcd(a,b): |
多表代换密码
1 | def cleanunalpha(cipher): |
LFSR
1 | def main(): |
RC4
1 | #-*- coding:utf-8 -*- |
DES
1 | # -*- coding: utf-8 -*- |
RSA
1 | import random |
MD5
1 | #-*- coding:utf-8 -*- |
综合实验
1 | #-*- coding:utf-8 -*- |
基于RSA和MD5的数字签名
1 | #-*- coding:utf-8 -*- |