0%

密码学课程设计之密码分析

发表于 更新于 分类于
本文字数： 2.7k 阅读时长 ≈ 2 分钟

密码学课程设计之密码分析

古典密码

单表代换密码

仿射密码属于单表代换密码，单表代换密码的密钥空间很小，同时它没有将字母出现的统计规律隐藏起来，因此使用统计分析法很快就可以进行破解。从这一点来说，汉语在加密方面的特性要远远优于英语，汉语中常用汉字就有3755个，而英语只有26个英文字母。
仿射密码加密算法为
$$
ye(x){\equiv}ax+b(mod26) 其中要求gcd(a，26)=1
$$
满足条件的a有12个，而b有26个，所以仿射加密的密钥空间大小为12*26=312。对于312种情况，现在的计算机通过暴力枚举的方法求解出正确的明文简直是小菜一碟。如果选择使用统计分析法，破解的速度应该会更快。
但对于普通置换密码和乘法密码相比之下，已经有了很大的改进与提高。

多表代换密码

维吉尼亚密码属于多表代换密码，多表代换密码打破了原语言的字符出现规律，故其分析比单表代换密码的分析要复杂得多。维吉尼亚加密的密钥空间大小为26m，对于一个相对小的m穷举也需要很长时间。

相较于单表代换，多表代换的安全性有了显著提高，需要猜测更多的字母表，并且频率分布特性也变得平坦。但多表代换密码也可以使用统计分析法破解，使用统计方法破解多表代换密码的前提是拦截到足够多的密文，这样才具备了统计分析的前提，所以对于传输量较小的明文加密，可以选择多表代换，比较安全。

序列密码

序列密码强度完全依赖于密钥序列的随机性和不可预测性。

密钥序列

密钥序列有需要具备以下功能：周期极大，均匀的n元分布，均匀的游程分布，良好的混乱性和扩散性。
由线性反馈移位寄存器所产生的序列中，像m序列具有良好的伪随机性，但它的密码强度很低，不过它的实现简单、速度快、由较为成熟的理论依据这些优点，现在在通信等工程技术中还是有广泛的应用。

LFSR周期分析

为了使LFSR生成最大周期序列，其生成多项式必须为本原多项式，当其阶为n时，应产生2n-1位长的伪随机序列。同时初态对输出序列的周期没有影响，其周期取决于lfsr所使用的反馈函数。

RC4安全性分析

RC4 算法容易用软件实现，加解密速度快（大约是 DES 的10倍）。

需要特别注意的是，为保证安全强度，目前的 RC4 至少要求使用 128 位密钥。

RC4 算法可看成一个有限状态自动机，大约有 21700种可能的状态。

分组密码

速度快、安全性较高、易于标准化和便于软硬件实现

DES安全性分析

  1. 互补性
    若
    $$
    c=E_k(m)
    $$
    则有
    $$
    \overline{c}=E_{\overline{k}}(\overline{m})
    $$
    在选择明文攻击下所需的工作量减半，仅需要测试256个密钥的一半就可以破解。

  2. 弱密钥
    对于加密解密运算没有区别的密钥叫弱密钥。

    如果k为弱密钥，则对于任意的64位数据m，有
    $$
    E_k(E_k(m))=m
    $$
    和
    $$
    D_k(D_k(m))=m
    $$
    有弱密钥产生是因为C、D存储的数据在循环移位时除位置外没有发生变化（C、D全为0或全为1）。

    此外还有半弱密钥，四分之一弱密钥和八分之一弱密钥，共256个。

    如果随机选取密钥，选中弱密钥的概率几乎可以忽略，但一般为了安全起见，在随机生成密钥后，要进行弱密钥检查，以保证不使用弱密钥作为DES的密钥。

  3. 迭代轮数
    对于低于16轮的DES已知明文攻击，差分分析攻击比穷举攻击有效。
    当DES进行到16轮迭代时，穷举攻击比差分分析攻击有效。

  4. 密钥长度
    DES密钥长度为56位，按照当时的计算能力，对于这个长度的密钥进行穷举攻击是不切实际的，但现在已经成为了现实。
    DES已经不足以保证敏感数据的安全，开始逐步退出历史舞台。
    人们针对DES设计了改进方法：多重DES。
    多重DES就是使用多个不同的DES密钥利用DES加密算法对明文进行多次加密。使用多重DES可以增加密钥量，从而大大提高抵抗对密钥的穷举搜索攻击的能力。

    1. 双重DES
      可以抵抗目前的穷举攻击，但无法抵抗中途相遇攻击，即获得一对明密文，使得一起从双方各自的起点出发，一段进行加密，另一端进行解密，当找到两端相同的时候，二重DES就被破解了。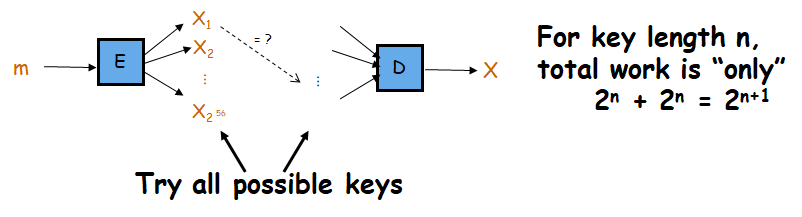

      1

    2. 三重DES

      1
      2
      3
      4
      5
      密钥长度增加到112位或168位
      增强了抗差分分析和线性分析的能力
      更换成本小
      处理速度较慢
      明文分组长度没有变化

      因此三重DES知识在DES变得不安全的情况下的一种临时解决方案。

公钥密码

RSA效率分析

由于RSA 的核心算法是模幂运算（大数自乘取模），要提高RSA 算法的效率，首要问题是提高模幂运算的效率。为了找到模幂运算的优化方法，我们不妨先来分析一般的模乘运算（两大数相乘取模），模乘过程中复杂度最高的环节是取模运算，因为一次除法实际上包含了多次加法、减法和乘法，如果在算法中能够尽量减少除法甚至避免除法，则算法的效率会大大提高。

RSA安全性分析

  1. 因子分解法

    RSA密码体制的安全性主要依赖于整数因子分解问题，试图分解模数n的素因子是攻击RSA最直接的方法。分解方法有试除法、 p−1因子分解法、p+1因子分解法、二次筛因子分解法、椭圆曲线因子分解法、数域筛因子分解法等。但由于因子分解的时间复杂性并没有降为多项式时间，因此，因子分解还是一个计算上的难题，只是需要考虑使用较大的位数，以确保无法在短时间内被破解。

  2. 针对参数选择的攻击

    1. 共模攻击

      多个用户使用相同的模数n，但公、私钥对不同。这种做法是不安全的。同样，不同用户选用的素因子p和q不能相同，因为n是公开的，如果素因子相同，可通过求模数n的公约数的方法得到相同素因子，从而分解模数n。

    2. 低指数攻击

      为了增强加密的高效性，希望选择较小的加密密钥e。如果相同的消息要送给多个实体，就不应该使用小的加密密钥。同样的，加密密钥d也不能取得太小。

    3. p-1和q-1都应有大的素数因子

RSA攻击防范措施

  1. 密钥长度

    密钥长度使用至少1024位，现在大部分使用1024*3位

  2. 参数选择

    1. 为避免椭圆曲线因子分解法，p和q的长度相差不能太大
    2. p和q的差值不应该太小
    3. gcd(p-1,q-1)应尽量小
    4. p和q应为强素数

Hash函数

MD5效率分析

MD5由MD4改进而来，但MD5的速度较MD4降低了近30%，在一般配置的PC机上使用MD5算法，处理1G的文件数据只需20-30秒（有些专用设备声称达 3GB/秒），不会对应用或机器带来过多负载，相对其他的哈希函数，其效率较好。

MD5安全性分析

Hash函数是将任意长度消息压缩成固定长度的”消息摘要“，所以它是一个多对一的函数，故必然存在”碰撞“，虽然概率很小。

从单向性考虑，虽然Hash函数是不可逆的，但是仍然可以使用某些方法从像推出原像，同时现在也有很多在线MD5解密网站。

Hash函数普遍容易遭受长度扩展攻击，就是在已知输入明文的长度和其 MD5 值的情况下，可以在明文后面附加任意内容，同时能够推算出新的正确的 MD5。