密码学复习
这个复习资料应该会有大量从ppt截的图(主要是自己懒的手打)
密码学基础
基本概念
密码编码学:研究密码编制的科学
密码分析学:研究密码破译的科学
主要任务
- 机密性
- 完整性
- 认证性(消息认证和实体认证)
- 不可否认性
基本思想
伪装信息 ,使未授权者不能理解它的含义
1 | 明⽂(plaintext,Message):伪装前的原始数据 |
密码体制(系统)
五元组(M,C,K,E,D)
1 | 明文空间M:全体明文的集合 |
简化模型
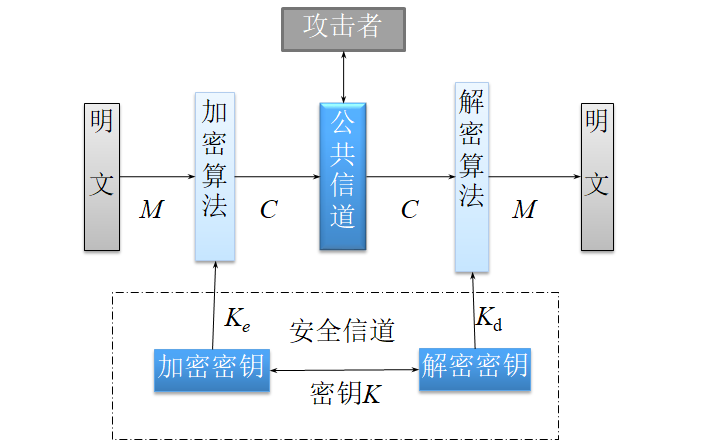
设计原理
科克霍夫原则:密码系统的安全性不应取决于不易改变的算法,而应取决于可随时改变的密钥
分类
对称密码:Kd=Ke或由其中一个很容易推出另一个
- 分组密码:DES,3DES,AES,IDEA
- 序列密码:RC4,A5
公钥密码:在计算上Kd不能由Ke推出,故可Ke公开
RSA,ECC,Rabin,Elgamal,NTRU
对比
对称密码优点
1 | 速度快 |
对称密码缺点
1 | 密钥分发需要安全通道 |
公钥密码优点
1 | 密钥分发相对容易 |
公钥密码缺点
1 | 加解密速度慢 |
密码分析
攻击者破译或攻击密码的方法
1 | 穷举攻击法 |
根据密码分析者对明⽂密⽂等数据资源的掌握程度 ,可以将密码分析攻分为以下几种类型
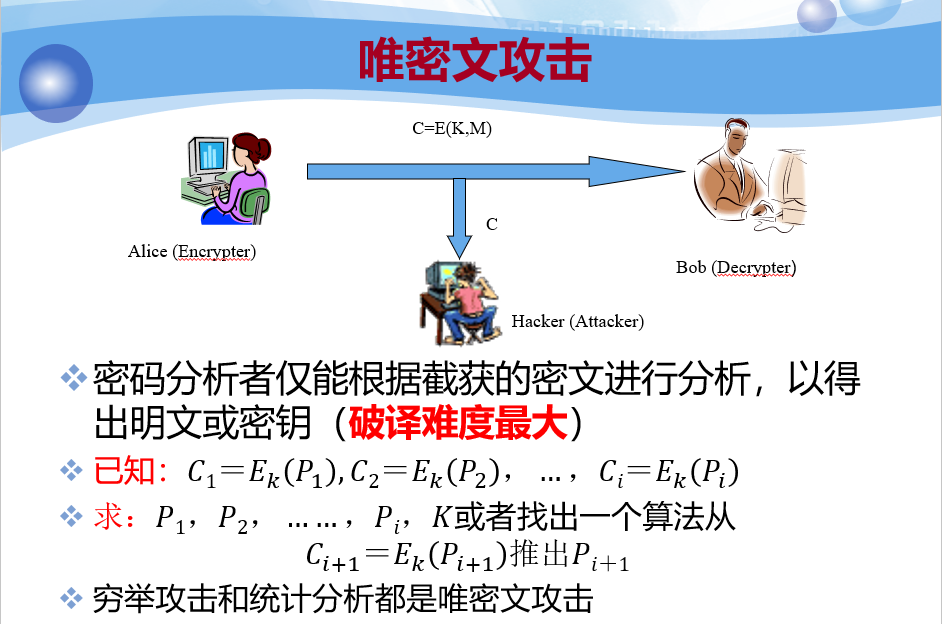
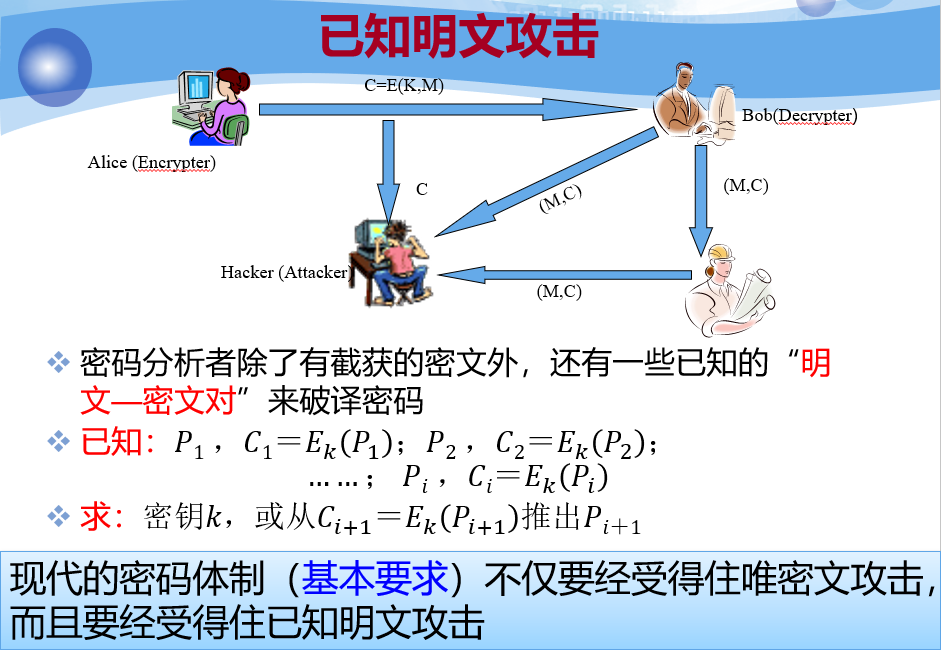
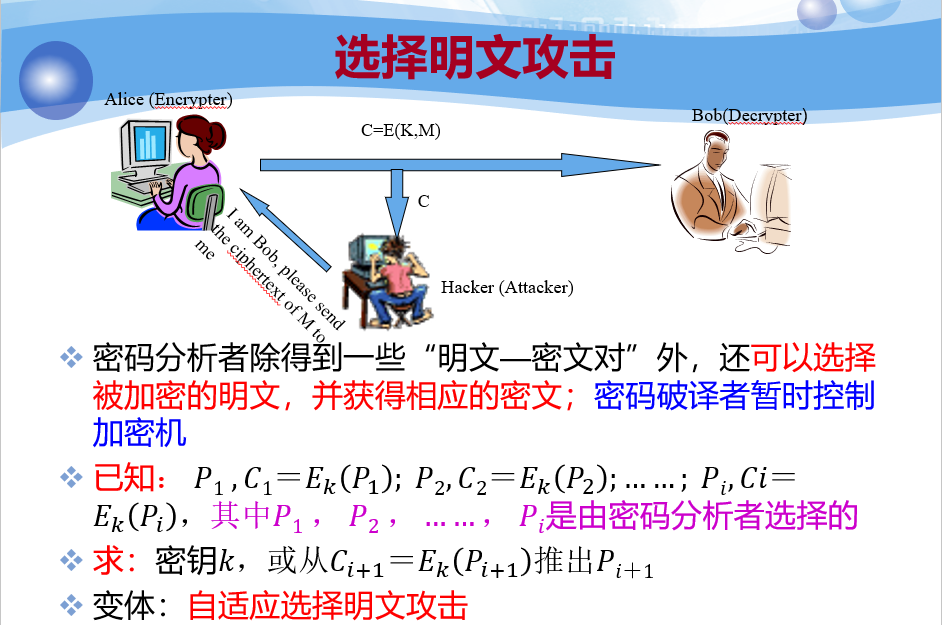
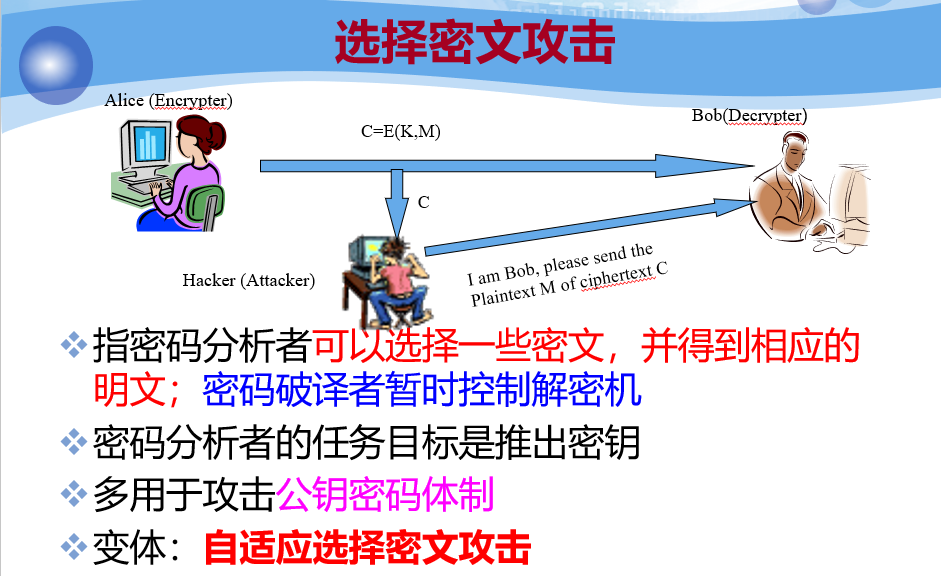
安全性
- 从密文恢复明文是困难的
- 从密文计算出明文部分信息是困难的
- 从密文探测出简单却有用的是事实困难的
评价密码体制安全性的不同途径
1 | 无条件安全性(理论安全) |
古典密码
替换密码:单表替换、多表替换
单表替换:移位代换密码、乘数密码、仿射密码
置换密码
替换密码
根据预先建立的替换表,将明文依次通过查表,替换为相应字符,生成密文。
单表替换:使用一个固定的替换表,明文、密文字符一一对应
多表替换:使用多个替换表
移位密码
加密:
$$
E_k(i){\equiv}(i+k)modq{\equiv}j
$$
其中
$$
0≤i,j<q,{k|0≤k<q}
$$
解密:
$$
D_k(j){\equiv}(j-k)modq{\equiv}i
$$
凯撒密码 k=3
字母-数字对应表
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
乘数密码
加密:
$$
E_k(i){\equiv}ikmodq{\equiv}j
$$
其中
$$
0≤j<q,gcd(k,q)=1
$$
解密:
$$
D_k(j){\equiv}j*k^{-1}modq{\equiv}i
$$
*仿射密码
加密:
$$
C{\equiv}(k_1m+k_2)mod26
$$
解密:
$$
M{\equiv}(c-k_2)*k_1^{-1}mod26
$$
*一次一密
每个明文字母都采用不同的替换表或密钥进行加密,理论上不可破译,却受到很大限制
1 | 密钥是真正的随机序列 |
维吉尼亚密码
密钥:
$$
k=k_1k_2k_3…k_m
$$
明文:
$$
k=k_1k_2k_3…k_m
$$
加密:
$$
E(m)=C=c_1c_2c_3…c_m
$$
$$
c_i{\equiv}m_i+k_imod26
$$
密钥:
$$
m_i{\equiv}c_i-k_imod26
$$
置换密码
明文字符集保持不变,但顺序被打乱
统计分析
任何自然语言都有固有的统计特性。如果这种统计特性在密文中有所反映,便可以通过分析明文和密文的统计规律来破译密码。许多古典密码都可用统计分析法破译
课本P56例3.10
P65.5.(5)
分组密码
概念
将明文划分成长为𝑚(如𝑚=64或128)的分组𝑃=(𝑝0, 𝑝1, 𝑝2, ….,𝑝(𝑚−1)),各明文分组分别在长为t的密钥𝐾=(𝑘0, 𝑘1, 𝑘2, ….,𝑘(𝑡−1)) 的控制下变换成长为𝑛的密文分组𝐶=(𝑐0, 𝑐1, 𝑐2, …,𝑐_(𝑛−1))。(一般 𝑚=𝑛)
原理
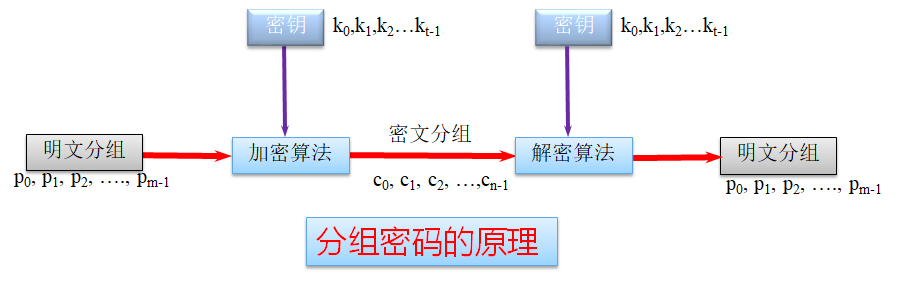
特点
速度快、安全性较高、易于标准化和便于软硬件实现
设计要求
- 分组长度要足够大
假设𝑛为分组长度,则要使2𝑛足够大,防止明文穷举攻击 - 密钥量要足够大
防止密钥穷举攻击 - 密码变换要足够复杂
使攻击者除穷举攻击外,找不到其他简洁的数学攻击方法 - 加密和解密运算简单
便于软件和硬件的实现 - 无数据扩展和压缩
三个基本原则
扩散(diffusion)
密钥或明文的每一比特变化影响密文的许多比特的变化,以便隐蔽明文的统计特性(形象的称为雪崩效应)
混淆(confusion)
又称混乱原则,指密钥和明文以及密文之间的依赖关系尽可能的复杂化,以防通过统计分析法进行破译(如使用非线性变换)
混乱必须是可逆的
乘积密码
多个密码复合的方法
两种迭代网络结构
Feistel网络
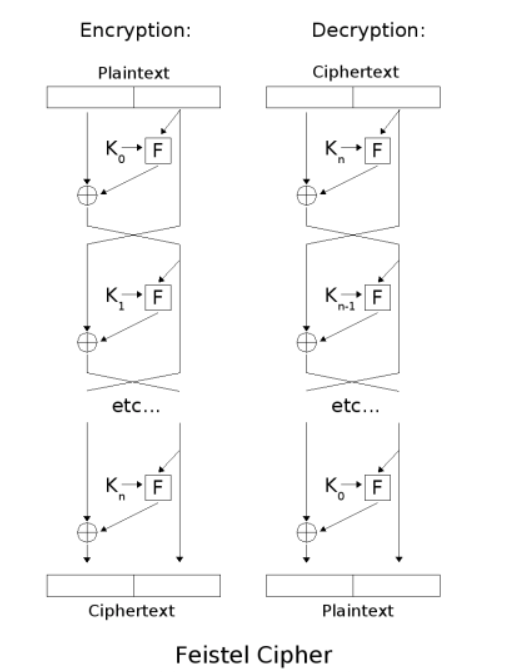
优点在于加解密相似性,它只需要一个逆转的密钥编排算法,其加解密部分几乎完全相同
SP网络
由S代换和P置换交替进行多次迭代形成的网络
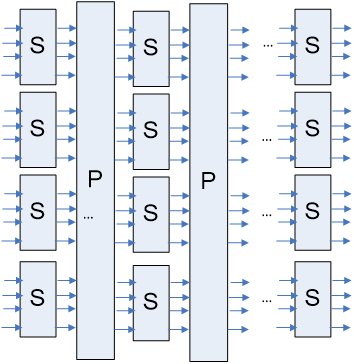
S盒起到混乱作用,P盒起到扩散的作用
轮函数F的设计准则
轮函数F是分组密码的核心,是分组密码中单轮加解密函数,其基本准则:
- 非线性(主要依赖S盒)
- 可逆性(能够实现解密)
- 雪崩效应
- 位独立(要求输入中某一位的变化,引起输出中其他位的变化应是彼此无关的)
其主要性能指标是安全性、速度、灵活性
子密钥的生成方法
子密钥的生成是从初始(种子)密钥产生迭代的各轮要使用的子密钥的算法。轮函数F的功能是在子密钥的参与和控制下实现的,其评价指标:
- 实现简单、速度满足要求
- 种子密钥的所有比特对每个子密钥比特的影响应大致相同
- 密钥和密文之间符合雪崩效应准则
- 没有弱密钥或弱密钥容易确定
迭代的轮数
决定迭代轮数的准则:使密码分析的难度大于简单穷举搜索攻击的难度
DES
算法过程
加密过程
$$
L_0R_0{\leftarrow}IP(<64位明文>)
$$
$$
L_i{\leftarrow}R_{i-1}
$$
$$
R_i{\leftarrow}L_{i-1}{\bigoplus}F(R_{i-1},K_i)
$$
$$
R_{16}{\leftarrow}L_{15}{\bigoplus}F(R_{15},K_{16})
$$
$$
L_{16}{\leftarrow}R_{15}
$$
$$
<64位密文>{\leftarrow}IP^{-1}(L_{16}R_{16})
$$
解密过程
$$
L_{16}R_{16}{\leftarrow}IP(<64位密文>)
$$
$$
R_{i-1}{\leftarrow}L_{i}{\bigoplus}F(R_{i},K_i)
$$
$$
L_{i-1}{\leftarrow}R_i
$$
$$
R_{0}{\leftarrow}L_{1}{\bigoplus}F(R_{1},K_{1})
$$
$$
L_{0}{\leftarrow}R_{1}
$$
$$
<64位明文>{\leftarrow}IP^{-1}(L_{0}R_{0})
$$
计算:S盒
查表,最高位和最低位对应行号,中间位对应列号。
安全性
互补性
弱密钥
双重、三重DES分析(加密的强度:密钥空间)
详见密码学课程设计之分组密码
AES
数学基础
AES中运算是按字节或(4字节的)字定义的
- 一个字节看成是系数在有限域GF(2)上的次数小于8的多项式(即看成有限域GF(28)中的一个元素)
- 一个字看成是系数在有限域GF(28) 上,且次数小于4的多项式





加解密流程
图1
字节代换(S 盒)
简单的查表。
逆:也是查表。
行移位
简单的移位。
第0行不变,第1行左移1个字节,第2行左移2个字节,第3行左移3个字节。
逆:变成右移。
列混合
这应该是 AES 考察的重中之重。
加法:异或
乘法两种方法:
- 用定义
- 用简便方法(乘2情况下)
- 最高位是0:直接左移1位。
- 最高位是1:左移1位后和
00011011异或。
乘3情况:(00000011=00000010⊕00000001)
逆:太难,不要求掌握。
轮密钥加
逐位异或。
密钥扩展
128 位密钥形成4个4字节组成的(32位)字:w[0],w[1],w[2],w[3] ,这是初始密钥加用到的。
扩充40个新列,以如下算法生成:
- 若 i不是4的倍数,那么 w[i]=w[i−4]⊕w[i−1]
- 若 i是4的倍数,那么 w[i]=w[i−4]⊕T(w[i−1])
其中,T()是一个很复杂的函数,定义如下:
- 字循环:循环左移一个字节,即有 [b0,b1,b2,b3]→[b1,b2,b3,b4]。
- 字节代换:用字节代换中的 S 盒,直接查表。
- 轮常量异或。
安全性分析
IDEA
SMS4
分组密码的工作模式
根据加密图画出解密图。
根据图写出算法。
错误传播分析。
电码本模式(ECB)
密码分组链接模式(CBC) **
**输出反馈模式(OFB)
密码反馈模式(CFB)
计数器模式(CTR)
序列密码
给定初始状态,写出输出序列。线性反馈移位寄存器(LFSR)。
周期、游程分析。
本原多项式、m序列。
详见密码学课程设计之序列密码
Hash 函数
基本概念
Hash 函数是密码学的一个重要分支,是将任意长度的输入变换为固定长度的输出的不可逆的单向密码体制。
性质
- 任意长度输入。
- 固定长度输出。
- 对于任意给定的消息x,计算H(x)比较容易,硬件软件都可实现。
- 单向性(抗原像性):从散列值h=H(m)推回消息m在计算上不可行。
- 抗弱碰撞性:对任意给定的消息x,找到y≠x且H(x)=H(y)在计算上不可行。
- 抗强碰撞性:找到任意满足H(x)=H(y)的两个不同消息x,y在计算上不可行。
数据填充
填充一个1和若干个0,使得消息长度模 512 与 448 同余。
特别注意:若原消息长度刚好满足这个条件,则再填充 512 位(1 个 1 和 511 个 0)。
填充完后再把原始消息长度以 64 比特表示附加在后面。
这样,最终消息长度恰好为 512 的整数倍。
MD5
分组长度为 512 比特,最终输出 128 位(即 16 字节,32 个十六进制位)的消息摘要。
过程为 4 轮,每轮 16 步,共 64 步。
SHA1
最终输出 160 位(即 20 字节,40 个十六进制位)的消息摘要。(因此比 MD5 抗穷举能力更强)
过程为 4 轮,每轮 20 步,共 80 步。
公钥密码
对称密码的局限性
密钥分发
通过安全信道分发密钥但安全信道不易实现密钥管理
n个用户每人需要存储n-1个密钥,故需要的总密钥为
$$
n*(n-1)/2
$$认证签名
通信双方共享密钥
1 | 接收方可以伪造原文——不能实现鉴别认证 |
尤其在电子商务等网络应用中
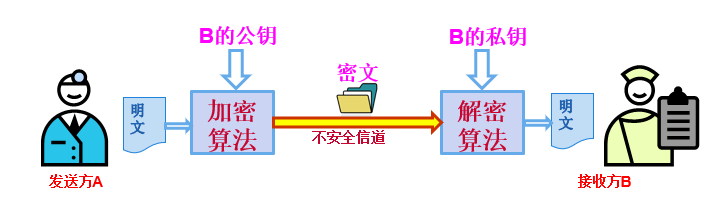
公钥密码体制(非对称密码)每个用户都分别拥有两个密钥加密密钥(公钥)和解密密钥(私钥),两者并不相同,且由加密密钥得到解密密钥在计算上不可行。
加密密钥是公开的
公钥密码体制示意图
1 | 发送方A查找接收方B的公钥 |
单向陷门函数f
- 给出f定义域中的任意元素x,计算f(x)是容易的
- 给出y=f(x)中的y,计算x:
- 若知道设计函数f时结合进去的某种信息(称为陷门),则x容易计算
- 若不知道该陷门信息,则x难以计算
公钥密码应满足的条件
解密算法D和加密算法E互逆,即对于所有明文M都有,
$$
D(E(M,K_e),K_d)=M
$$由Ke求出Kd在计算上不可行
算法E和D都是高效的
公钥密码体制RSA
该算法的数学基础时初等数论中的欧拉定理,其安全性是基于大整数因子分解的困难性
算法描述
密钥的生成
选择两个大素数 𝑝和𝑞,(𝑝≠𝑞,需要保密,步骤4以后建议销毁)
计算
$$
n=p×q,\varphi(n)=(p-1)×(q-1)
$$选择整数e使
$$
(\varphi(n),e)=1,1<e<\varphi(n)
$$计算d,使
$$
d=e^{-1}mod\varphi(n)
$$
得到:公钥为{e,n};私钥为{d}
加密(用e,n):明文M<n,密文
$$
C=M^e(modn)
$$解密(用d,n):密文C,明文
$$
M=C^d(modn)
$$
正确性
例题
素数的生成
一般的,选取一个素数的过程如下:
1 | 随机选一个奇数𝑛(如使用伪随机数产生器) |
快速实现am(mod n)
模重复平方法
安全性
对RSA的攻击
1 | 针对n分解的攻击 |
针对n分解的攻击
试除法
完全尝试所有小于根号n的素数二次筛法
找出正整数x,y,使得
$$
x^2{\equiv}y^2(modn)
$$
即存在整数c,满足
$$
cn=(x-y)(x+y)
$$
并且满足
$$
x{\neq}{\pm}y(modn)
$$
因此,n是
$$
x^2-y^2=(x-y)(x+y)
$$
的因子,即
$$
gcd(x+y,n)或gcd(x-y,n)
$$
均为n的因子,即可分解n
循环攻击

循环攻击实例


同模攻击

在使用RSA公钥密码通信中,不同用户的密钥不能有相同的模值
选择密文攻击
RSA模幂运算的性质:
$$
E_k(ab)=E_K(a)E_K(b)
$$- 破译密文

- 骗取签名

低加密指数攻击
小的公钥可加快加密的速度,但过小的公钥易受到攻击
时间攻击
针对RSA核心运算是非常耗时的模乘,只要能够精确监视RSA的解密过程,就能估计出私钥d,但实际操作困难。
注意问题
1 | 选择素数𝑝和𝑞时,应使其欧拉函数p-1和q-1的最小公倍数尽可能大(p-1和q-1有大的素因子)。最小公倍数越大,幂剩余函数的周期就越长—避免循环攻击 |
公钥密码体制ElGamal
安全性是基于离散对数问题
算法描述
- 密钥的生成

- 加密

- 解密
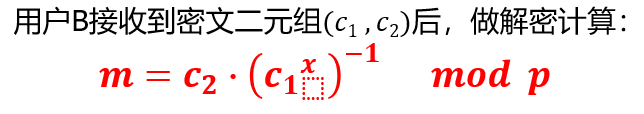
正确性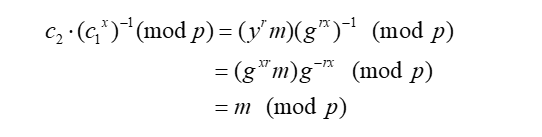
特点
- 非确定性
由于密文依赖于加密过程中用户A选择的随机数r,所以加密相同的明文可能会产生不同的密文——概率加密 - 密文空间大于明文空间
明文空间为Zp,而密文空间为Zp× Zp
安全性
离散对数问题的求解
1 | 大步-小步法 |
大步-小步法

指数积分法


例题


公钥密码体制ECC
不知道考不考,考了再整理叭
基于身份的加密体制IBE
同ECC
中间人攻击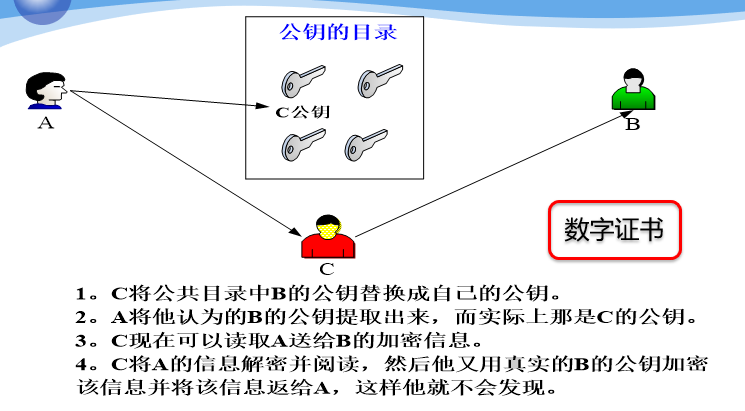
公钥密码体制分析
公钥密码分析
1 | 蛮力攻击。防范措施——长密钥。但从实用性角度,要考虑折衷 |
优点(跟对称密码相比)
1 | 密钥分发简单 |
不足(跟对称密码相比)
1 | 公钥密码算法比对称密码算法慢 |
混合加密
公钥加密和私钥加密的合理结合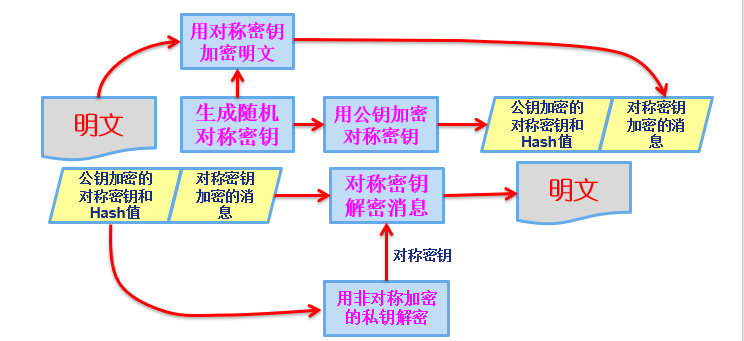
数字签名技术
数字签名(Digital Signature),也称电子签名,是指附加在某一电子文档中的一组特定的符号或代码,它是利用数学方法和密码算法对该电子文档进行关键信息提取并进行加密而形成的,用于标识签发者的身份以及签发者对电子文档的认可,并能被接收者用来验证该电子文档在传输过程中是否被篡改或伪造
签名用私钥,验证用公钥 。
RSA
ElGamal(如果考会给出算法)
特殊:盲签名
安全性分析
若不加 Hash 会怎么样?(没有Hash函数有什么缺点?)
可以伪造签名。
看P246 6.
正确性分析
密码协议
联系《密码学课程设计》的综合实验。
对称密码用到的密钥用公钥密码体制传输。
- Alice 用 Bob 的公钥加密对称密码的密钥,发送给 Bob 。
- Bob 用自己的私钥解密,得到密钥。
给出具体密码协议,分析合理性,验证可靠性,证明安全性。
综合,会涉及到前面学的。