0%

密码学课程设计之Hash函数

发表于 更新于 分类于
本文字数： 5.2k 阅读时长 ≈ 5 分钟

密码学课程设计之Hash函数

Hash，一般翻译做散列、杂凑，或音译为哈希，是把任意长度的输入（又叫做预映射pre-image）通过散列算法变换成固定长度的输出，该输出就是散列值。这种转换是一种压缩映射，也就是，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，所以不可能从散列值来确定唯一的输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。

MD5

算法描述

MD5算法的输入是长度小于264比特的消息，输出为128比特的消息摘要。输入消息以512比特的分组为单位处理，流程图如下

1

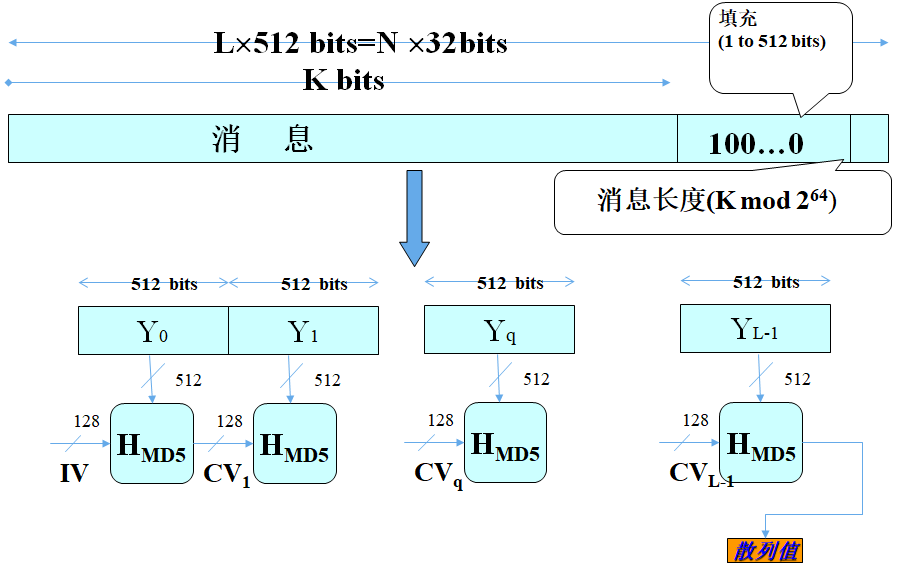
具体过程

附加填充位

使消息长度模512=448，如果消息长度模512恰等于448，增加512个填充比特。即填充的个数为1~512。

需要特别注意的是，若原始消息长度刚好满足模 512 与 448 同余，则还需要填充 1 个 1 和 511 个 0 。

填充方法：第1比特为1，其余全部为0

补足长度

将消息长度转换为64比特的数值。

如果长度超过64比特所能表示的数据长度，值保留最后64比特。

添加到填充数据后面，使数据为512比特的整数倍。

512比特按32比特分为16组。

64比特消息长度

先将消息长度写成 64 bit ，长度不足64位消息自行填充，然后变换成小端序

1
2
3
length = Little_endian(bin(lm%(2**64))[2:].zfill(64),False)
    message += length
    lm = len(message)

初始化链接变量

MD5使用4个32位的寄存器A,B,C和D，最开始存放4个固定的32位的整数参数，即初始链接变量。

1
a,b,c,d= (0x67452301, 0xefcdab89, 0x98badcfe, 0x10325476)#小端序

2

这里为了方便，可以将小端序封装成一个函数，用来将二进制或十六进制组成的字符串转成小端序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def Little_endian(s,Hex):
    l = len(s)
    ans = ""
    if Hex == False:
        i = l-8
        while i >= 0:
            ans += s[i:i+8]
            i -= 8
    else:
        i = l-2
        while i >= 0:
            ans += s[i:i+2]
            i -= 2
    return ans

分组处理

由4轮组成，512比特的消息分组Mi被均分为16个子分组参与每轮16步函数运算。

2

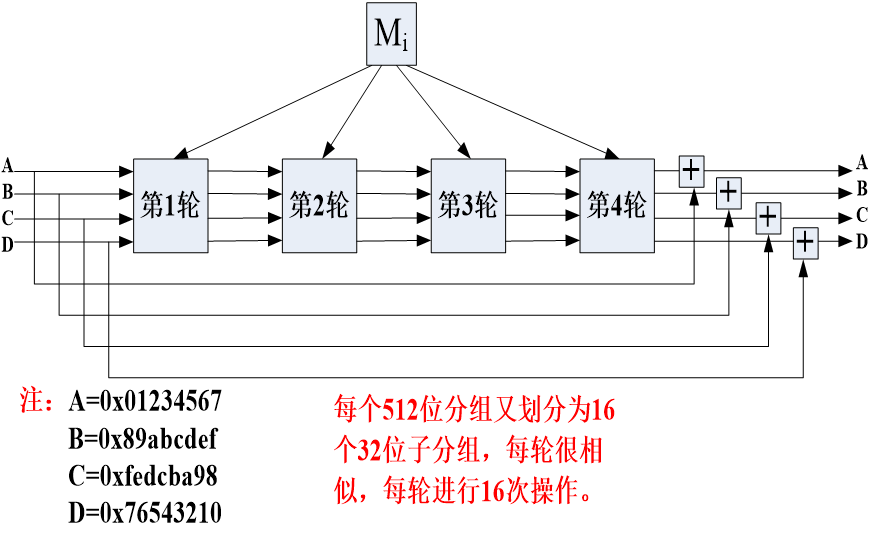
步函数

3

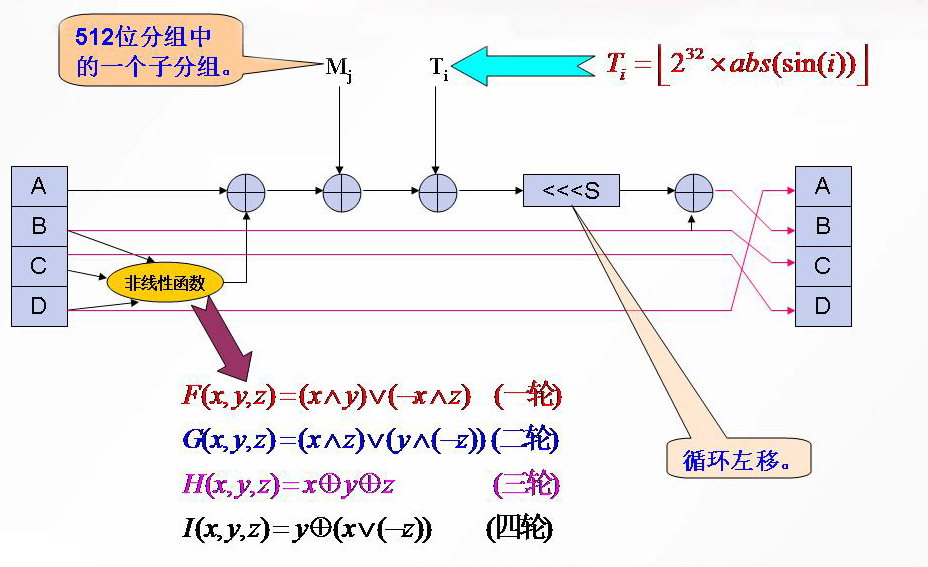
上一步的D，B，C直接赋给下一步的A，C，D，而上一步的A需要进行变换赋给B。

这里的加法都是模232加法，为了方便起见，封装封装！！！

1
2
def mod32(a,b):
    return (a+b)%(2**32)

A先与分线性函数变换结果相加，再和M[j]相加，再与T[i]想加，循环左移s位，最后于原来的B相加，得到新的B。

非线性函数

见上图

使用lambda表达式来写

1
2
3
4
F = lambda x,y,z:((x&y)|((~x)&z))
G = lambda x,y,z:((x&z)|(y&(~z)))
H = lambda x,y,z:(x^y^z)
I = lambda x,y,z:(y^(x|(~z)))

M[j]

表示消息分组Mi的第j(0≤j≤15)个32比特子分组。

第一轮以字的初始次序使用

后面三轮的次序由下面置换确定
$$
P_2(i)=(1+5i)mod16
$$

$$
P_3(i)=(5+3i)mod16
$$

$$
P_4(i)=7imod16
$$

在程序中我们直接打表

1
2
3
4
5
#每次 M[i]次序。
M = ((0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15),
     (1,6,11,0,5,10,15,4,9,14,3,8,13,2,7,12),
     (5,8,11,14,1,4,7,10,13,0,3,6,9,12,15,2),
     (0,7,14,5,12,3,10,1,8,15,6,13,4,11,2,9))

T[i]

常数 T[i]为
$$
2^{32}×abs(sin(i))=[4294967296×abs(sin(i))]
$$
其中i为弧度（1≤i≤64）

循环左移

打表

1
2
3
4
5
6
L = lambda x,n:(((x<<n)|(x>>(32-n)))&(0xffffffff))
#循环左移位数
R = ((7,12,17,22,7,12,17,22,7,12,17,22,7,12,17,22),
     (5,9,14,20,5,9,14,20,5,9,14,20,5,9,14,20),
     (4,11,16,23,4,11,16,23,4,11,16,23,4,11,16,23),
     (6,10,15,21,6,10,15,21,6,10,15,21,6,10,15,21,))

输出

如果所有512分组操作完毕，输出
$$
A‖B‖C‖D
$$
即为消息的MD5值(消息摘要)

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
#-*- coding:utf-8 -*-
#Python2
import math

#初始向量
a,b,c,d= (0x67452301, 0xefcdab89, 0x98badcfe, 0x10325476)
# A, B, C, D = (0x01234567, 0x89ABCDEF, 0xFEDCBA98, 0x76543210)

#非线性函数
F = lambda x,y,z:((x&y)|((~x)&z))
G = lambda x,y,z:((x&z)|(y&(~z)))
H = lambda x,y,z:(x^y^z)
I = lambda x,y,z:(y^(x|(~z)))

#循环左移
L = lambda x,n:(((x<<n)|(x>>(32-n)))&(0xffffffff))

#循环左移的位移位数
R = ((7,12,17,22,7,12,17,22,7,12,17,22,7,12,17,22),
     (5,9,14,20,5,9,14,20,5,9,14,20,5,9,14,20),
     (4,11,16,23,4,11,16,23,4,11,16,23,4,11,16,23),
     (6,10,15,21,6,10,15,21,6,10,15,21,6,10,15,21,))

#每次 M[i]（消息分片）次序。
M = ((0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15),
     (1,6,11,0,5,10,15,4,9,14,3,8,13,2,7,12),
     (5,8,11,14,1,4,7,10,13,0,3,6,9,12,15,2),
     (0,7,14,5,12,3,10,1,8,15,6,13,4,11,2,9))

# 将大端序二进制/十六进制字符串转成小端序
# Hex == True means Hex, Hex == False means Bin
def Little_endian(s,Hex):
    l = len(s)
    ans = ""
    if Hex == False:
        i = l-8
        while i >= 0:
            ans += s[i:i+8]
            i -= 8
    else:
        i = l-2
        while i >= 0:
            ans += s[i:i+2]
            i -= 2
    return ans

# 将字符串转成二进制字符串
def str2Bin(s):
    return "".join('{:08b}'.format(ord(x)) for x in s)

# 模2的32次方加
def mod32(a,b):
    return (a+b)%(2**32)

# 产生常数T[i]，常数有可能超过32位，需要&0xffffffff操作
# 返回的是十进制的数。
def T(i):
    result = (int(4294967296*abs(math.sin(i))))&0xffffffff
    return result

# Calculate the MD5 value
def MD5(message):
    #字符串转二进制字符串
    message = str2Bin(message)
    lm = len(message)
    #附加填充位
    lm_mod = lm%512
    #若原始消息长度刚好满足模512与448同余
    #则还需要填充512位
    if lm_mod == 448:
        FillLength = 512
    elif lm_mod > 448:
        FillLength = 512+448-lm_mod
    else:
        FillLength = 448-lm_mod
    message += '1'+(FillLength-1)*'0'
    #填充原始消息长度
    length = Little_endian(bin(lm%(2**64))[2:].zfill(64),False)
    message += length
    lm = len(message)
    #生成初始变量
    A,B,C,D = a,b,c,d
    for i in range(0,lm,512):
        Y = message[i:i+512]
        for j in range(4):  # 共4轮
            for k in range(16): # 每轮16个步骤
                #记录初始状态
                AA,BB,CC,DD = A,B,C,D
                #非线性函数
                if j == 0:
                    t = F(B,C,D)
                elif j == 1:
                    t = G(B,C,D)
                elif j == 2:
                    t = H(B,C,D)
                else:
                    t = I(B,C,D)
                T_i = T(16*j+k+1)
                M_j = Little_endian(Y[M[j][k]*32:M[j][k]*32+32],False)
                A, C, D = DD, BB, CC
                B = mod32(AA,t)
                B = mod32(B,int(M_j,2))
                B = mod32(B,T_i)
                B = L(B,R[j][k])
                B = mod32(B,BB)
                print str(16*j+k+1).zfill(2),
                print hex(A).replace("0x","").replace("L","").zfill(8),
                print hex(B).replace("0x","").replace("L","").zfill(8),
                print hex(C).replace("0x","").replace("L","").zfill(8),
                print hex(D).replace("0x","").replace("L","").zfill(8)
    ans1 = Little_endian(hex(mod32(A,a))[2:-1],True).zfill(8)
    ans2 = Little_endian(hex(mod32(B,b))[2:-1],True).zfill(8)
    ans3 = Little_endian(hex(mod32(C,c))[2:-1],True).zfill(8)
    ans4 = Little_endian(hex(mod32(D,d))[2:-1],True).zfill(8)
    return ans1+ans2+ans3+ans4

def main():
    print "请输出你要加密的密文:".decode('utf-8').encode('gbk')
    message = raw_input()
    # m = "Beijing University of Posts and Telecommunications"
    ans = MD5(message)
    print "MD5加密之后的结果:".decode('utf-8').encode('gbk')
    print ans

if __name__ == '__main__':
    main()

效率分析

MD5由MD4改进而来，但MD5的速度较MD4降低了近30%，在一般配置的PC机上使用MD5算法，处理1G的文件数据只需20-30秒（有些专用设备声称达 3GB/秒），不会对应用或机器带来过多负载，相对其他的哈希函数，其效率较好。

安全性分析

Hash函数是将任意长度消息压缩成固定长度的”消息摘要“，所以它是一个多对一的函数，故必然存在”碰撞“，虽然概率很小。

从单向性考虑，虽然Hash函数是不可逆的，但是仍然可以使用某些方法从像推出原像，同时现在也有很多在线MD5解密网站。

Hash函数普遍容易遭受长度扩展攻击，就是在已知输入明文的长度和其 MD5 值的情况下，可以在明文后面附加任意内容，同时能够推算出新的正确的 MD5。