0%

密码学课程设计之公钥密码

发表于 更新于 分类于
本文字数： 4.6k 阅读时长 ≈ 4 分钟

密码学课程设计之公钥密码

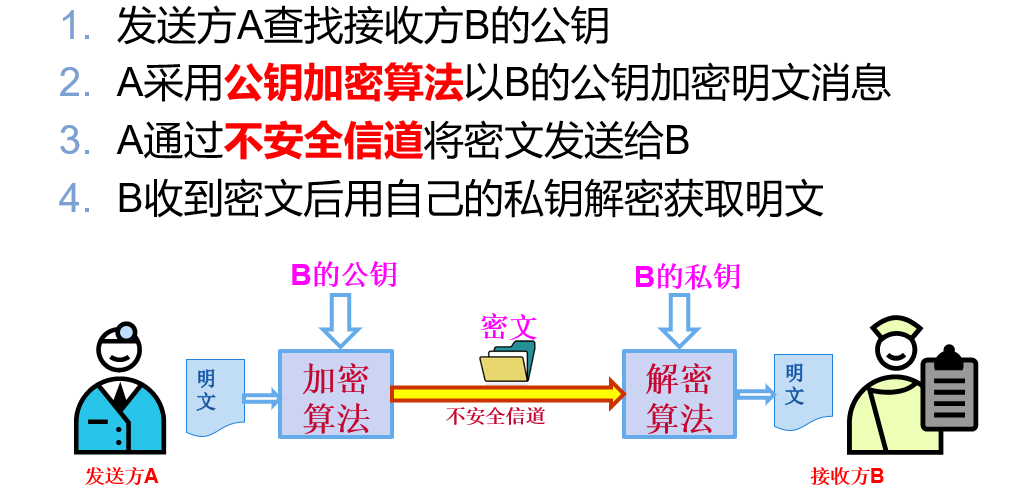
公钥密码 又称为非对称密码，拥有公钥密码的用户分别拥有加密密钥和解密密钥。通过加密密钥不能得到解密密钥。并且加密密钥是公开的。

1

RSA

该算法的数学基础是初等数论中的欧拉定理。

其安全性基于大整数因子分解的困难性。

算法描述

  1. 密钥的生成

    1. 选择两个大素数 𝑝和𝑞,（𝑝≠𝑞，需要保密，步骤4以后建议销毁）

    2. 计算
      $$
      n=p×q,\varphi(n)=(p-1)×(q-1)
      $$

    3. 选择整数e使
      $$
      (\varphi(n),e)=1,1<e<\varphi(n)
      $$

    4. 计算d，使
      $$
      d=e^{-1}mod\varphi(n)
      $$
      得到：公钥为{e,n}；私钥为{d}

  1. 加密（用e，n）：明文M<n，密文
    $$
    C=M^e(modn)
    $$

  2. 解密（用d，n）：密文C，明文

$$
M=C^d(modn)
$$

密钥的生成

这一步是整个RSA最重要的一步，其安全性就是基于大整数因子分解的困难，所以，选择两个大素数p和q就显得尤为重要！！！

那么，怎么选择呢？

一般的，选取一个素数的过程如下

1
2
3
随机选一个奇数𝑛(如使用伪随机数产生器)
用某种概率性算法（如Miller-Rabin算法）对𝑛进行一次素性检验，如果𝑛没有通过检验，转到步骤1
重复步骤2足够多次，如果𝑛都通过了检测，则认为𝑛为素数

Miller-Rabin素数测试算法

费马小定理

设p是一个素数，则对任意整数a，有
$$
a^p{\equiv}a(modp)
$$
二次探测

如果p是一个素数，0<x<p，则方程
$$
x^2{\equiv}1(modp)
$$
的解为
$$
x=1或x=p-1
$$

要测试N是否为素数，首先将N−1分解为2sd。在每次测试开始时，先随机选一个介于[1,N−1]的整数a，之后如果对所有的r∈[0,s−1]，若ad mod N ≠ 1且a2rd mod N ≠ −1，则N是合数；否则，N有3/4的概率为素数。

增加测试的次数，该数是素数的概率会越来越高。

具体操作：先用randrange()函数生成一个大伪随机数，然后再用Miller-Rabin素数测试算法判断它是不是素数，若是则就用它；不是则再随机生成一个新的伪随机数，再判断，直到找到可以用的大伪随机数p和q。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#Miller_Rabin算法
def miller_rabin(a,n):
    temp=n-1
    j=0
    while temp&1==0:
        temp=temp>>1
        j+=1
    x=fast_mod(a,temp,n)
    if x==1 or x==n-1:
        return True
    while j:
        x=fast_mod(x,2,n)
        if x==n-1:
            return True
        j-=1
    return False

  #判断是否为素数
def is_prime(n):
    times=100
    if n==2:
        return True
    if n<2 or n%2==0:
        return False
    i=1
    while i<=times:
        a=random.randint(1,n-2)+1
        if miller_rabin(a,n)==False:
            return False
        i+=1
    return True
    
#生成素数
def create_prime():
    while True:
        p=random.randrange(1<<512,1<<1024,3)
        if(is_prime(p)):
            return p

模重复平方计算法

快速求幂运算

1
2
3
4
5
6
7
8
9
def fast_mod(b,n,m):
    a=1
    while n!=0:
        temp=n&1
        n=n>>1
        if temp==1:
            a=(a*b)%m
        b=(b*b)%m
    return a

公钥e的选择

$$
(\varphi(n),e)=1,1<e<\varphi(n)
$$

在RSA算法中，e和(p-1)*(q-1)互质的条件容易满足，如果选择较小的e，则加、解密的速度加快，也便于存储，但会导致安全问题。

为了减少加密运算时间，很多人采用尽可能小的e值，如3。但是已经证明低指数将会导致安全问题，故此，一般选择e为16位的素数，可以有效防止攻击，又有较快速度。

1
2
3
4
5
6
7
8
9
10
11
12
def E(fn):
    while True:
        e=random.randint(1<<16,fn)
        temp=e
        t=fn
        d=1
        while d!=0:
           d=t%temp
           t=temp
           temp=d
        if t==1:
            return e

计算私钥d

$$
d=e^{-1}mod\varphi(n)
$$

这里使用扩展欧几里得法求逆元

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def D(e,fn):
    r1,r2=e,fn
    s1,s2=1,0
    t1,t2=0,1
    while(r2 > 0):
        q=r1//r2
        r= r1-q*r2
        r1=r2
        r2=r
        s=s1-q*s2
        s1=s2
        s2=s
        t=t1-q*t2
        t1=t2
        t2=t
    return s1%fn

加解密

加密
$$
C=M^e(modn)
$$

1
2
def RSA_encrypt(e,n,plaintext):
    return fast_mod(plaintext,e,n)

解密
$$
M=C^d(modn)
$$

1
2
def RSA_decrypt(d,n,ciphertext):
    return fast_mod(ciphertext,d,n)

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
import random
import math

#Miller-Rabin测试：不断选取不超过n-1的基b(s次)，
#计算是否每次都有bn-1 ≡ 1(mod n)，若每次都成立则n是素数，否则为合数。
#Miller_Rabin算法
def miller_rabin(a,n):
    temp=n-1
    j=0
    while temp&1==0:
        temp=temp>>1
        j+=1
    x=fast_mod(a,temp,n)
    if x==1 or x==n-1:
        return True
    while j:
        x=fast_mod(x,2,n)
        if x==n-1:
            return True
        j-=1
    return False

  #判断是否为素数
def is_prime(n):
    times=100
    if n==2:
        return True
    if n<2 or n%2==0:
        return False
    i=1
    while i<=times:
        a=random.randint(1,n-2)+1
        if miller_rabin(a,n)==False:
            return False
        i+=1
    return True


#模重复平方计算法
def fast_mod(b,n,m):
    a=1
    while n!=0:
        temp=n&1
        n=n>>1
        if temp==1:
            a=(a*b)%m
        b=(b*b)%m
    return a

#生成素数
def create_prime():
    while True:
        p=random.randrange(1<<512,1<<1024,3)
        if(is_prime(p)):
            return p

#生成公钥，随机得到小素数，（e，Φ（n）)=1
def E(fn):
    while True:
        e=random.randint(1<<16,fn)
        temp=e
        t=fn
        d=1
        while d!=0:
           d=t%temp
           t=temp
           temp=d
        if t==1:
            return e

#计算私钥,e求逆，欧几里得扩展算法
def D(e,fn):
    r1,r2=e,fn
    s1,s2=1,0
    t1,t2=0,1
    while(r2 > 0):
        q=r1//r2
        r= r1-q*r2
        r1=r2
        r2=r
        s=s1-q*s2
        s1=s2
        s2=s
        t=t1-q*t2
        t1=t2
        t2=t
    return s1%fn

#RSA加密
def RSA_encrypt(e,n,plaintext):
    return fast_mod(plaintext,e,n)

#RSA解密
def RSA_decrypt(d,n,ciphertext):
    return fast_mod(ciphertext,d,n)
#测试
p=create_prime()
q=create_prime()
print('当前选取的大素数p为:%d'%p)
print('当前选取的大素数q为:%d'%q)
n=p*q
fn=(p-1)*(q-1)
e=E(fn)
d=D(e,fn)
print('当前生成的公钥e为:%d'%e)
print('当前生成的私钥d为:%d'%d)

plaintext=random.randint(1<<512,1<<1024)
print('随机生成的明文为:%d'%plaintext)

ciphertext=RSA_encrypt(e,n,plaintext)
print('RSA加密后的结果为:%d'%ciphertext)

plaintext=RSA_decrypt(d,n,ciphertext)
print('RSA解密后的结果为:%d'%plaintext)

效率分析

由于RSA 的核心算法是模幂运算（大数自乘取模），要提高RSA 算法的效率，首要问题是提高模幂运算的效率。为了找到模幂运算的优化方法，我们不妨先来分析一般的模乘运算（两大数相乘取模），模乘过程中复杂度最高的环节是取模运算，因为一次除法实际上包含了多次加法、减法和乘法，如果在算法中能够尽量减少除法甚至避免除法，则算法的效率会大大提高。

安全性分析

  1. 因子分解法

    RSA密码体制的安全性主要依赖于整数因子分解问题，试图分解模数n的素因子是攻击RSA最直接的方法。分解方法有试除法、 p−1因子分解法、p+1因子分解法、二次筛因子分解法、椭圆曲线因子分解法、数域筛因子分解法等。但由于因子分解的时间复杂性并没有降为多项式时间，因此，因子分解还是一个计算上的难题，只是需要考虑使用较大的位数，以确保无法在短时间内被破解。

  2. 针对参数选择的攻击

    1. 共模攻击

      多个用户使用相同的模数n，但公、私钥对不同。这种做法是不安全的。同样，不同用户选用的素因子p和q不能相同，因为n是公开的，如果素因子相同，可通过求模数n的公约数的方法得到相同素因子，从而分解模数n。

    2. 低指数攻击

      为了增强加密的高效性，希望选择较小的加密密钥e。如果相同的消息要送给多个实体，就不应该使用小的加密密钥。同样的，加密密钥d也不能取得太小。

    3. p-1和q-1都应有大的素数因子

攻击防范措施

  1. 密钥长度

    密钥长度使用至少1024位，现在大部分使用1024*3位

  2. 参数选择

    1. 为避免椭圆曲线因子分解法，p和q的长度相差不能太大
    2. p和q的差值不应该太小
    3. gcd(p-1,q-1)应尽量小
    4. p和q应为强素数