0%

密码学课程设计之序列密码

发表于 更新于 分类于
本文字数： 3.4k 阅读时长 ≈ 3 分钟

密码学课程设计之序列密码

密钥序列

序列密码强度完全依赖于密钥序列的随机性和不可预测性。

密钥序列有需要具备以下功能：周期极大，均匀的n元分布，均匀的游程分布，良好的混乱性和扩散性。
由线性反馈移位寄存器所产生的序列中，像m序列具有良好的伪随机性，但它的密码强度很低，不过它的实现简单、速度快、由较为成熟的理论依据这些优点，现在在通信等工程技术中还是有广泛的应用。

线性反馈移位寄存器

选择一个15次以上的不可约多项式，编写一个线性反馈移位寄存器。验证生成序列的周期。

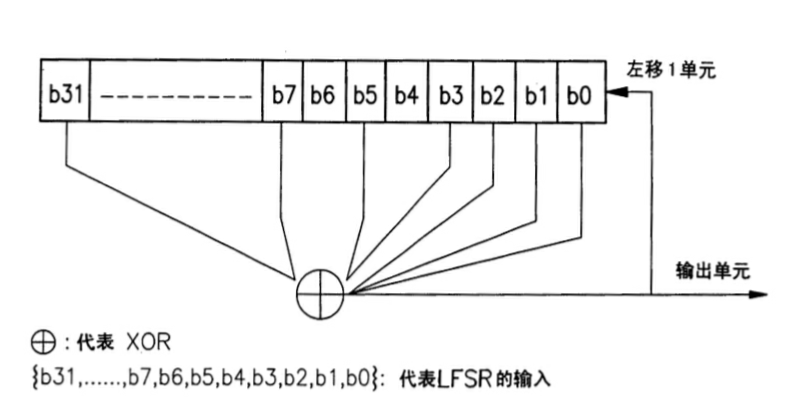
LFSR图示如下

1

附上百度百科本原多项式词条中常用本原多项式

常用本原多项式

此处选择了n=16的本原多项式
$$
x^{16}+x^{12}+x^3+x+1
$$
验证生成序列的周期即验证n级LFSR的输出序列在重复之前能够参产生2n-1位长的伪随机序列（除去全0的情况）。

附上代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def main():
    print("请输入寄存器(16位)的初始状态")
    s=input()
    if s=='0000000000000000' or len(s)!=16:
        print("输入有误，请重新输入")
        return main()
    #s='0000000000000110'
    ss=s
    s1=list(s)#字符串转列表
    cycle=0
    while True:
    #选择不可约多项式 x^16+x^12+x^3+x+1 
        i=int(s1[15])^int(s1[11])^int(s1[2])^int(s1[0])
    #左移一位
        for j in range(len(s1)):
            s1[len(s1)-1-j]=s1[len(s1)-2-j]
        #添加异或结果
        s1[0]=str(i)
        s2="".join(s1)#列表转字符串
        cycle+=1
        #print(s2)
        if s2==ss:
            #print(s2)
            break
    print("周期为：",cycle)
    if cycle==pow(2,len(s))-1:
        print("验证成功！")
    else:
        print("验证失败！")

if __name__ == '__main__':
    main()

LFSR周期分析

为了使LFSR生成最大周期序列，其生成多项式必须为本原多项式，当其阶为n时，应产生2n-1位长的伪随机序列。同时初态对输出序列的周期没有影响，其周期取决于LFSR所使用的反馈函数。

RC4

RC4是一个典型的基于非线性数组变换的序列密码。它以一个足够大的数组为基础，对其进行非线性变换，产生密钥序列，一般把这个大数组称为S盒。

RC4包含两个处理过程：

1
2
密钥调度算法KSA，用来置乱S盒的初始排列
伪随机生成算法PRGA，用来输出随机序列并修改S的当前排列顺序

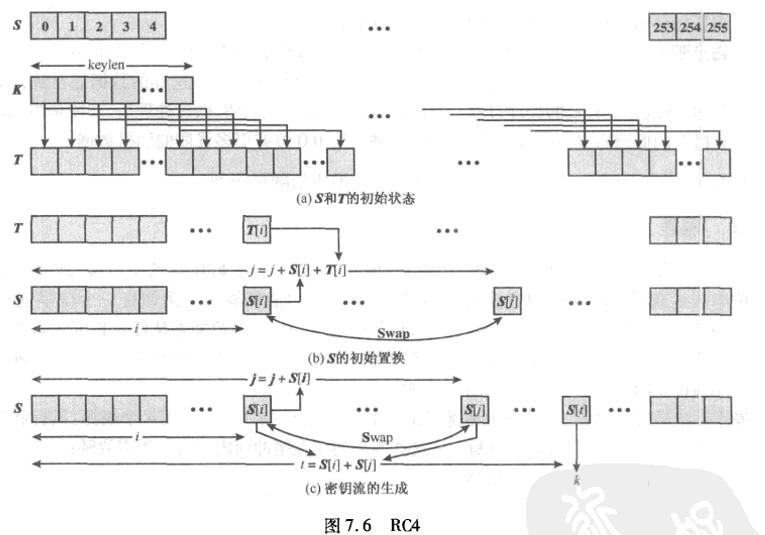
RC4流程图

KSA

KSA首先初始化S，即S[i]=i(i=0~255)，同时建立一个临时数组向量T(|T|=256)，如果种子密钥K的长度为256字节，则直接将K赋给T，否则，若种子密钥K的长度小于|T|，则将K的值赋给T的前|K|个元素，并不断重复加载K的值，直到T被填满。

1
2
3
4
5
6
lk = len(key)
S = [0] * 256#S数组S
T=''#临时向量T
for i in range(256) :
    S[i] = i#S赋初值
    T += key[i%lk]#T赋初值，填充满T

用T产生S的初始置换，从S[0]到S[255]，对每个S[i]，根据T[i]的值将S[i]与S中的另一个字节对换。

1
2
3
4
j = 0
for i in range(256):
    j = (j+S[i]+ord(T[i]))%256
    S[i],S[j] = S[j],S[i]

PRGA

从S中随机选取一个元素输出，并置换S以便下一次选取，选取过程取决于索引i和j，最后加解密都是将k与明文或密文字节异或。

1
2
3
4
5
6
7
8
9
10
11
i = j = 0
    ans = ""
    for x in text:
        i = (i+1)%256
        j = (j+S[i])%256
        S[i],S[j] = S[j],S[i]
        t = (S[i]+S[j])%256
        k = S[t]
        #加密时，将k与明文异或；解密时，k与密文异或
        ans += chr(ord(x)^k)
    return ans

最后用base64编码一下就okk了。

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#-*- coding:utf-8 -*-
import base64
def RC4(text,key):
    ## 将0到255的互不重复的元素装入S盒。
    lk = len(key)
    S = [0] * 256#S数组S
    T=''#临时向量T
    for i in range(256) :
        S[i] = i#S赋初值
        T += key[i%lk]#T赋初值，填充满T
    ## 根据密钥打乱S盒
    j = 0
    for i in range(256):
        j = (j+S[i]+ord(T[i]))%256
        S[i],S[j] = S[j],S[i]
    ## 生成伪随机数，构造密文
    i = j = 0
    ans = ""
    for x in text:
        i = (i+1)%256
        j = (j+S[i])%256
        S[i],S[j] = S[j],S[i]
        t = (S[i]+S[j])%256
        k = S[t]
        #加密时，将k与明文异或；解密时，k与密文异或
        ans += chr(ord(x)^k)
    return ans
# RC4加密: 明文转成base64编码的密文
def RC4Encrypt(message,key):
    return base64.b64encode(RC4(message,key))
# RC4解密: base64编码的密文转成明文
def RC4Decrypt(cipher,key):
    return RC4(base64.b64decode(cipher),key)
# 对字符串的加密解密
def main():
    print "1.加密".decode('utf-8').encode('gbk')
    print "2.解密".decode('utf-8').encode('gbk')
    mode=raw_input()
    if mode=='1':
    ## 加密
        try:
            fin = open("E:\Cryptology\RC4\Plaintext.txt",'r')
            fout = open("E:\Cryptology\RC4\Plainouttext.txt","w")
            s = fin.read()
            k = "LGDISTHEBEST"
            print "文件读取成功！".decode('utf-8').encode('gbk')
            fout.write(RC4Encrypt(s,k))
            print "文件加密成功！".decode('utf-8').encode('gbk')
            fin.close()
            fout.close()
        except IOError:
            print "文件读取失败！！！".decode('utf-8').encode('gbk')
    ## 解密
    if mode=='2':
        try:
            fin = open("E:\Cryptology\RC4\Ciphertext.txt",'r')
            fout = open("E:\Cryptology\RC4\Cipherouttext.txt","w")
            s = fin.read()
            k = "LGDISTHEBEST"
            print "文件读取成功！".decode('utf-8').encode('gbk')
            fout.write(RC4Decrypt(s,k))
            print "文件解密成功！".decode('utf-8').encode('gbk')
            fin.close()
            fout.close()
        except IOError:
            print "文件读取失败！！！".decode('utf-8').encode('gbk')
if __name__ == '__main__':
    main()

RC4安全性分析

RC4 算法容易用软件实现，加解密速度快（大约是 DES 的10倍）。

需要特别注意的是，为保证安全强度，目前的 RC4 至少要求使用 128 位密钥。

RC4 算法可看成一个有限状态自动机，大约有 21700种可能的状态。

小声哔哔一句：我们老干爹是不可战胜的

WESG中国区冠军！

LGD牛逼！

1